Verdad de axiomas: ¿Cómo se comprueba su validez?

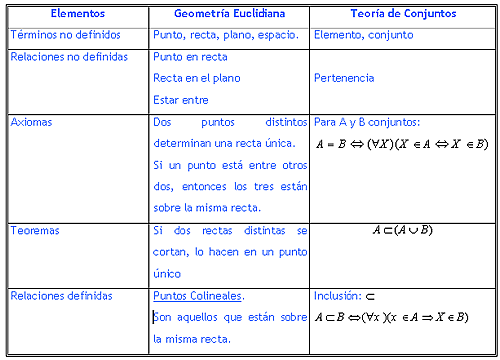
Los axiomas son declaraciones fundamentales que se aceptan como verdaderas sin necesidad de demostración. Son los principios básicos sobre los que se construye un sistema lógico o matemático. Sin embargo, ¿cómo sabemos que estos axiomas son verdaderos? ¿Cómo se comprueba su validez?

En este artículo exploraremos las diferentes formas en que se puede comprobar la verdad de los axiomas y cómo esto afecta a la validez de un sistema lógico.

¿Qué son los axiomas?

Antes de entrar en cómo se comprueba su validez, es importante entender qué son los axiomas. Los axiomas son proposiciones que se aceptan como verdaderas sin necesidad de demostración. Son el punto de partida para cualquier sistema lógico o matemático.

Los axiomas son necesarios porque no se puede demostrar todo. Si se intentara demostrar todo a partir de otros principios, se entraría en un proceso infinito y nunca se llegaría a una conclusión. Por lo tanto, los axiomas son una forma de detener este proceso y establecer un punto de partida.

Comprobando la validez de los axiomas

Para comprobar la validez de los axiomas, hay dos enfoques principales: el enfoque empírico y el enfoque lógico.

Enfoque empírico

El enfoque empírico se basa en la observación y la experiencia. Se trata de comprobar si los axiomas se corresponden con la realidad. Por ejemplo, el axioma "la tierra es redonda" se puede comprobar empíricamente observando su forma desde el espacio.

Este enfoque es especialmente útil en áreas como la física o la biología, donde se pueden hacer experimentos para comprobar la verdad de los axiomas.

Enfoque lógico

El enfoque lógico se basa en la coherencia interna del sistema lógico. Se trata de comprobar si los axiomas son coherentes entre sí y si se pueden deducir las teoremas a partir de ellos.

Este enfoque es especialmente útil en áreas como la matemática o la lógica, donde se puede demostrar la verdad de los teoremas a partir de los axiomas.

La importancia de la validez de los axiomas

La validez de los axiomas es fundamental para la validez de todo el sistema lógico o matemático. Si los axiomas son falsos, entonces todo lo que se deduzca a partir de ellos también será falso.

Por lo tanto, es importante comprobar la verdad de los axiomas antes de utilizarlos como base para un sistema lógico o matemático.

Conclusión

Los axiomas son proposiciones fundamentales que se aceptan como verdaderas sin necesidad de demostración. Para comprobar su validez, se pueden utilizar dos enfoques principales: el enfoque empírico y el enfoque lógico.

La validez de los axiomas es fundamental para la validez de todo el sistema lógico o matemático. Por lo tanto, es importante comprobar la verdad de los axiomas antes de utilizarlos como base para un sistema lógico o matemático.

Preguntas frecuentes

1. ¿Se pueden modificar los axiomas?

Sí, los axiomas pueden ser modificados si se encuentran pruebas empíricas o lógicas que los contradigan. Por ejemplo, el axioma "la tierra es plana" fue modificado a "la tierra es redonda" después de la observación empírica de su forma desde el espacio.

2. ¿Qué pasa si un axioma es falso?

Si un axioma es falso, entonces todo lo que se deduzca a partir de él también será falso. Por lo tanto, es fundamental comprobar la verdad de los axiomas antes de utilizarlos como base para un sistema lógico o matemático.

3. ¿Cómo se pueden comprobar los axiomas en áreas como la filosofía?

En áreas como la filosofía, los axiomas pueden ser más difíciles de comprobar empíricamente. En este caso, se utiliza principalmente el enfoque lógico para comprobar la coherencia interna del sistema lógico o filosófico.

4. ¿Se pueden tener diferentes axiomas para el mismo sistema lógico?

Sí, es posible tener diferentes axiomas para el mismo sistema lógico. Por ejemplo, existen diferentes sistemas lógicos para la matemática, como la aritmética de Peano y la aritmética de Zermelo-Fraenkel.

5. ¿Por qué son importantes los axiomas en la lógica y la matemática?

Los axiomas son importantes en la lógica y la matemática porque son el punto de partida para todo el sistema lógico o matemático. Si los axiomas son falsos, entonces todo lo que se deduzca a partir de ellos también será falso. Por lo tanto, es fundamental comprobar la verdad de los axiomas antes de utilizarlos como base para un sistema lógico o matemático.