Trigonometría básica: descubre las razones de 30, 45 y 60 grados
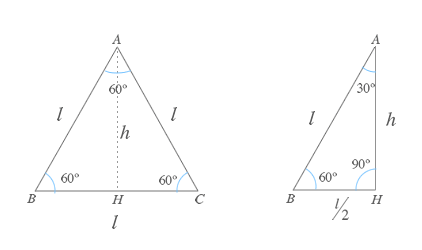
La trigonometría es una rama de las matemáticas que se encarga del estudio de las relaciones entre los ángulos y los lados de un triángulo. En la trigonometría básica, una de las primeras cosas que se aprenden son las razones de los ángulos de 30, 45 y 60 grados. En este artículo, descubrirás qué son estas razones y cómo se utilizan en la resolución de problemas trigonométricos.
¿Qué son las razones trigonométricas?
Las razones trigonométricas son relaciones entre los lados de un triángulo rectángulo y sus ángulos. Hay tres razones trigonométricas básicas: seno, coseno y tangente. Cada una de estas razones se representa con una letra: seno (sin), coseno (cos) y tangente (tan).
El triángulo rectángulo
Antes de entrar en detalle sobre las razones trigonométricas de los ángulos de 30, 45 y 60 grados, es importante entender qué es un triángulo rectángulo. Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90 grados. Los otros dos ángulos pueden ser agudos (menores a 90 grados) u obtusos (mayores a 90 grados).
En un triángulo rectángulo, el lado opuesto al ángulo recto se llama hipotenusa, mientras que los otros dos lados se llaman catetos.
Razones trigonométricas de 30 grados
El ángulo de 30 grados es uno de los ángulos más comunes en la trigonometría básica. La razón trigonométrica del ángulo de 30 grados es:
- Seno de 30 grados (sin 30°) = 1/2
- Coseno de 30 grados (cos 30°) = √3/2
- Tangente de 30 grados (tan 30°) = 1/√3
Para recordar estas razones, puedes utilizar la siguiente analogía: imagina que tienes una pizza y la divides en seis porciones iguales. Si tomas una porción de esa pizza, tendrás un ángulo de 30 grados. La mitad de la pizza (tres porciones) serían el seno de 30 grados, mientras que la mitad de la pizza más un tercio (cuatro porciones) serían el coseno de 30 grados. La tangente de 30 grados sería el resultado de dividir el seno entre el coseno.
Razones trigonométricas de 45 grados
El ángulo de 45 grados es otro de los ángulos más comunes en la trigonometría básica. La razón trigonométrica del ángulo de 45 grados es:
- Seno de 45 grados (sin 45°) = √2/2
- Coseno de 45 grados (cos 45°) = √2/2
- Tangente de 45 grados (tan 45°) = 1
Para recordar estas razones, puedes imaginar que tienes un cuadrado con diagonales. Si trazas una línea desde el centro del cuadrado hasta uno de los lados, tendrás un ángulo de 45 grados. La razón trigonométrica del seno y el coseno de 45 grados son iguales y valen la mitad de la diagonal del cuadrado. La tangente de 45 grados es igual a 1, ya que la longitud del cateto opuesto y del cateto adyacente son iguales.
Razones trigonométricas de 60 grados
El ángulo de 60 grados es el más complejo de los tres ángulos que estamos viendo en este artículo, ya que involucra la raíz cuadrada de 3. La razón trigonométrica del ángulo de 60 grados es:
- Seno de 60 grados (sin 60°) = √3/2
- Coseno de 60 grados (cos 60°) = 1/2
- Tangente de 60 grados (tan 60°) = √3
Para recordar estas razones, puedes imaginar que tienes un triángulo equilátero (un triángulo con tres lados iguales y tres ángulos iguales de 60 grados). Si trazas una línea desde el centro del triángulo hasta uno de los lados, tendrás un ángulo de 60 grados. El seno de 60 grados es la altura del triángulo equilátero dividida por dos. El coseno de 60 grados es la mitad de uno de los lados del triángulo equilátero. La tangente de 60 grados es la raíz cuadrada de 3 (la altura del triángulo equilátero) dividida por la mitad de uno de los lados.
Conclusión
Las razones trigonométricas de los ángulos de 30, 45 y 60 grados son fundamentales en la trigonometría básica. A través de analogías simples y fáciles de recordar, puedes aprender estas razones y utilizarlas en la resolución de problemas trigonométricos.
Preguntas frecuentes
¿Cómo se relacionan las razones trigonométricas con los ángulos?
Las razones trigonométricas son relaciones entre los lados de un triángulo rectángulo y sus ángulos. Cada ángulo tiene una razón trigonométrica asociada (seno, coseno y tangente), que se calcula dividiendo la longitud de uno de los lados del triángulo por la longitud de otro lado.
¿Qué es un triángulo rectángulo?
Un triángulo rectángulo es aquel que tiene un ángulo de 90 grados. Los otros dos ángulos pueden ser agudos (menores a 90 grados) u obtusos (mayores a 90 grados). En un triángulo rectángulo, el lado opuesto al ángulo recto se llama hipotenusa, mientras que los otros dos lados se llaman catetos.
¿Cómo se calcula la tangente de un ángulo?
La tangente de un ángulo se calcula dividiendo el seno del ángulo por el coseno del ángulo. Es decir, tan θ = sin θ / cos θ.
¿Qué es un ángulo agudo?
Un ángulo agudo es aquel que tiene una medida menor a 90 grados.
¿Cómo se utiliza la trigonometría en la vida cotidiana?
La trigonometría se utiliza en la vida cotidiana en situaciones como la medición de distancias, la determinación de alturas y la resolución de problemas de navegación. También es fundamental en campos como la física, la ingen
Deja una respuesta