Teorema en acción: ejemplos prácticos para aplicar en tu día a día

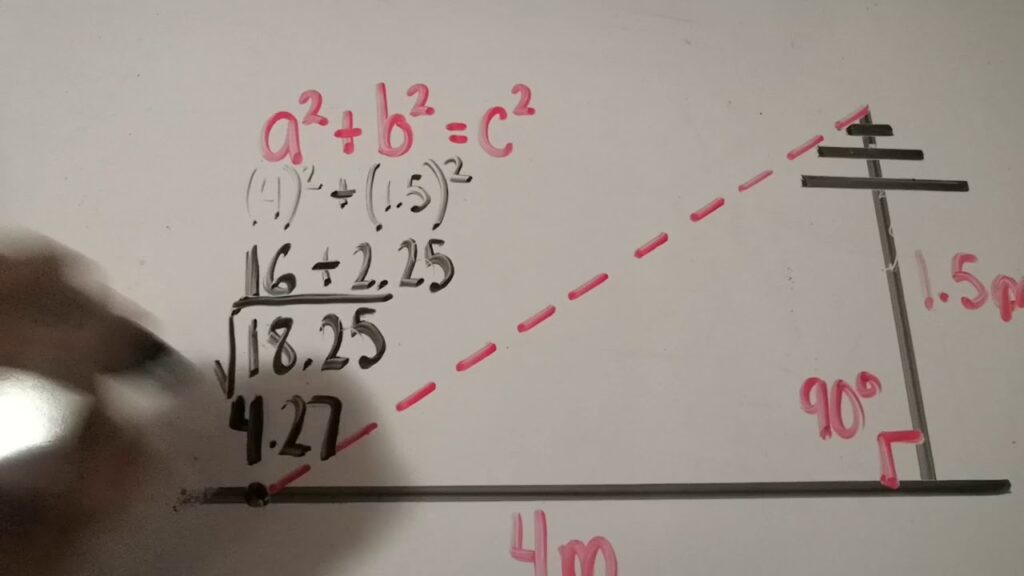
¿Alguna vez has escuchado hablar del teorema? Es una herramienta matemática que nos permite demostrar que algo es cierto o falso. Pero, ¿cómo podemos aplicarlo en nuestra vida diaria? En este artículo, te mostraremos algunos ejemplos prácticos de cómo utilizar el teorema en el día a día.

1. Comprobar si un número es par o impar

Uno de los ejemplos más simples de teorema es comprobar si un número es par o impar. Para hacerlo, simplemente debemos aplicar el teorema de la división. Si un número es divisible entre dos, entonces es par. Si no lo es, entonces es impar.

2. Demostrar que un triángulo es equilátero

Otro ejemplo práctico de teorema es demostrar que un triángulo es equilátero. Para hacerlo, podemos aplicar el teorema de Pitágoras. Si los tres lados del triángulo son iguales, entonces podemos utilizar el teorema de Pitágoras para demostrar que los ángulos internos también son iguales.

3. Comprobar si un conjunto de números es par o impar

Continuando con el primer ejemplo, podemos utilizar el teorema de la suma para comprobar si un conjunto de números es par o impar. Si la suma de los números es par, entonces el conjunto es par. Si la suma de los números es impar, entonces el conjunto es impar.

4. Demostrar que una función es continua

El teorema del valor intermedio nos permite demostrar que una función es continua. Si una función cumple con este teorema, entonces podemos asegurar que no tiene saltos ni interrupciones en su trayectoria.

5. Comprobar si un número es primo

El teorema de Wilson nos permite comprobar si un número es primo o no. Si un número cumple con este teorema, entonces podemos asegurar que es primo. De lo contrario, no lo es.

6. Demostrar que un polinomio tiene raíces reales

El teorema de Descartes nos permite demostrar que un polinomio tiene raíces reales. Si un polinomio cumple con este teorema, entonces podemos asegurar que tiene al menos una raíz real.

7. Comprobar si una figura es simétrica

El teorema de la simetría nos permite comprobar si una figura es simétrica o no. Si una figura cumple con este teorema, entonces podemos asegurar que tiene un eje de simetría.

8. Demostrar que una serie converge

El teorema de la convergencia nos permite demostrar que una serie converge. Si una serie cumple con este teorema, entonces podemos asegurar que su suma es finita.

9. Comprobar si un triángulo es rectángulo

El teorema de Pitágoras también nos permite comprobar si un triángulo es rectángulo. Si los lados de un triángulo cumplen con este teorema, entonces podemos asegurar que uno de sus ángulos es recto.

10. Demostrar que una matriz es invertible

El teorema de la inversión nos permite demostrar que una matriz es invertible. Si una matriz cumple con este teorema, entonces podemos asegurar que tiene una matriz inversa.

11. Comprobar si un conjunto es vacío

El teorema de la existencia nos permite comprobar si un conjunto es vacío o no. Si un conjunto cumple con este teorema, entonces podemos asegurar que tiene al menos un elemento.

12. Demostrar que un sistema de ecuaciones tiene solución única

El teorema de Rouché-Frobenius nos permite demostrar que un sistema de ecuaciones tiene solución única. Si un sistema de ecuaciones cumple con este teorema, entonces podemos asegurar que tiene una solución única.

13. Comprobar si dos conjuntos son equivalentes

El teorema de la equivalencia nos permite comprobar si dos conjuntos son equivalentes. Si dos conjuntos cumplen con este teorema, entonces podemos asegurar que tienen la misma cardinalidad.

14. Demostrar que una función es biyectiva

El teorema de la biyección nos permite demostrar que una función es biyectiva. Si una función cumple con este teorema, entonces podemos asegurar que es inyectiva y sobreyectiva.

15. Comprobar si un número es racional o irracional

El teorema de la irracionalidad nos permite comprobar si un número es racional o irracional. Si un número cumple con este teorema, entonces podemos asegurar que es irracional.

Conclusión

El teorema es una herramienta muy útil en matemáticas, pero también lo es en nuestra vida diaria. Con estos ejemplos prácticos, podemos ver cómo podemos aplicar el teorema en situaciones cotidianas y tomar decisiones más informadas y precisas en base a ello.

Preguntas frecuentes

1. ¿Es el teorema solo para matemáticas?

No necesariamente. El teorema es una herramienta matemática, pero se puede aplicar en otras áreas como la física, la biología y la economía.

2. ¿Cómo puedo aprender más sobre teoremas?

Hay muchas fuentes de información sobre teoremas, desde libros y cursos en línea hasta videos y tutoriales en línea.

3. ¿Qué habilidades necesito para aplicar los teoremas en mi vida diaria?

No necesitas habilidades especiales para aplicar los teoremas en tu vida diaria. Solo necesitas entender la teoría detrás de ellos y cómo aplicarla a situaciones cotidianas.

4. ¿Por qué es importante aprender sobre teoremas?

Aprender sobre teoremas puede ayudarte a tomar decisiones más informadas y precisas en tu vida diaria. También puede ayudarte a entender mejor el mundo que te rodea y las leyes que lo rigen.

5. ¿Los teoremas solo son útiles para los matemáticos?

No, los teoremas son útiles para cualquier persona que quiera tomar decisiones más informadas y precisas en su vida diaria.