Teorema de Ptolomeo: solución a figuras geométricas complejas
Si eres un apasionado de las matemáticas y estás interesado en la geometría, probablemente hayas oído hablar del teorema de Ptolomeo. Este teorema es uno de los más importantes de la geometría clásica y es utilizado para calcular la medida de los lados y los ángulos de figuras geométricas complejas.
En este artículo, te explicaremos en qué consiste el teorema de Ptolomeo y cómo puedes utilizarlo para resolver figuras geométricas complejas. Además, te daremos algunos ejemplos para que puedas entender mejor su aplicación.
¿Qué es el teorema de Ptolomeo?
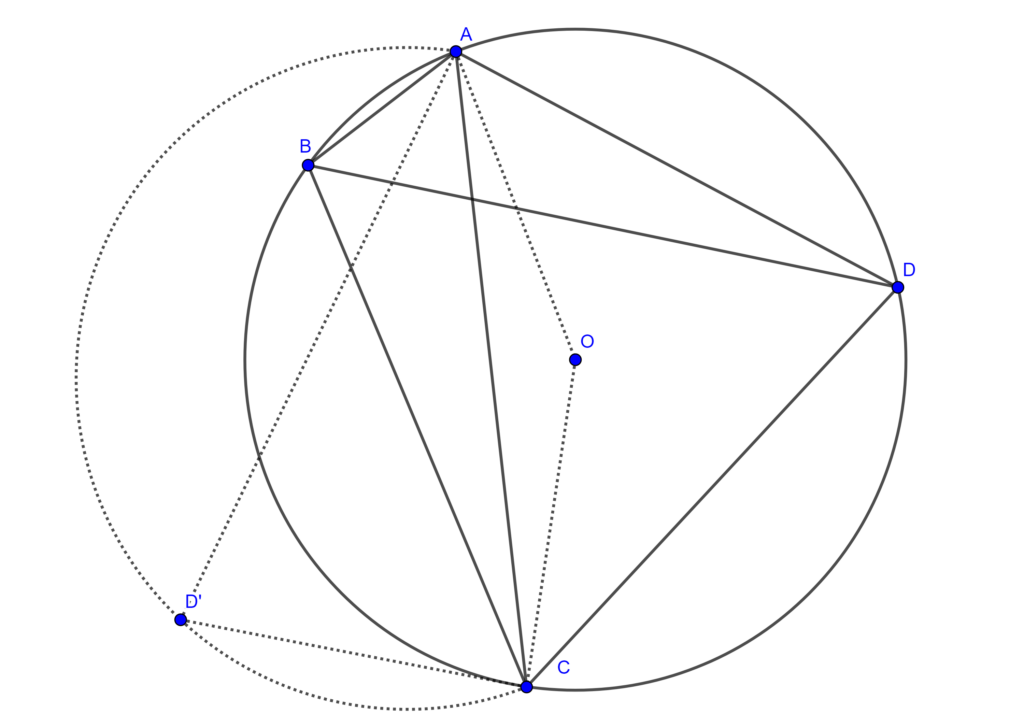
El teorema de Ptolomeo es un teorema de la geometría euclidiana que establece una relación entre los lados y los ángulos de un cuadrilátero cíclico. Un cuadrilátero cíclico es aquel que puede ser inscrito en una circunferencia.
La relación establecida por el teorema de Ptolomeo es la siguiente:
a · c + b · d = e · f
Donde a, b, c y d son los lados del cuadrilátero cíclico y e y f son las diagonales que se cruzan en el centro de la circunferencia que lo contiene.
¿Cómo se aplica el teorema de Ptolomeo?
Para aplicar el teorema de Ptolomeo, es necesario conocer la medida de tres de los lados del cuadrilátero cíclico y la medida de una de sus diagonales. A partir de esta información, se puede calcular la medida del cuarto lado y la otra diagonal.
Para entender mejor su aplicación, veamos un ejemplo:
Supongamos que tenemos un cuadrilátero cíclico ABCD, donde AB = 3 cm, BC = 4 cm y CD = 5 cm. Además, conocemos la medida de la diagonal AC, que es de 6 cm.
Para calcular la medida del lado AD, podemos utilizar el teorema de Ptolomeo de la siguiente manera:
3 · 5 + 4 · x = 6 · 6
15 + 4x = 36
4x = 21
x = 5.25
Por lo tanto, la medida del lado AD es de 5.25 cm.
Ejemplos de aplicación del teorema de Ptolomeo
Veamos algunos ejemplos más para entender mejor cómo se aplica el teorema de Ptolomeo:
Ejemplo 1:
Calcula la medida del lado AB de un cuadrilátero cíclico si conocemos que BC = 3 cm, CD = 4 cm y AD = 5 cm.
Solución:
Utilizando el teorema de Ptolomeo, tenemos:
5 · 3 + x · 4 = 3 · 4
15 + 4x = 12
4x = -3
x = -0.75
Como no puede haber medidas negativas, podemos concluir que el cuadrilátero no es cíclico y por lo tanto, no se puede calcular la medida del lado AB.
Ejemplo 2:
Calcula la medida de la diagonal AC de un cuadrilátero cíclico si conocemos que AB = 3 cm, BC = 4 cm, CD = 5 cm y AD = 6 cm.
Solución:
Utilizando el teorema de Ptolomeo, tenemos:
3 · 5 + 4 · 6 = x · 5
15 + 24 = 5x
39 = 5x
x = 7.8
Por lo tanto, la medida de la diagonal AC es de 7.8 cm.
Conclusión
El teorema de Ptolomeo es una herramienta muy útil para resolver figuras geométricas complejas, principalmente cuadriláteros cíclicos. Conociendo la medida de tres de los lados de la figura y la medida de una de sus diagonales, es posible calcular la medida del cuarto lado y la otra diagonal.
Es importante recordar que el cuadrilátero debe ser cíclico para poder aplicar el teorema de Ptolomeo. Si no lo es, no se puede calcular la medida de los lados o las diagonales.
Preguntas frecuentes
1. ¿Qué es un cuadrilátero cíclico?
Un cuadrilátero cíclico es aquel que puede ser inscrito en una circunferencia.
2. ¿En qué consiste el teorema de Ptolomeo?
El teorema de Ptolomeo establece una relación entre los lados y los ángulos de un cuadrilátero cíclico.
3. ¿Cómo se aplica el teorema de Ptolomeo?
Para aplicar el teorema de Ptolomeo, es necesario conocer la medida de tres de los lados del cuadrilátero cíclico y la medida de una de sus diagonales. A partir de esta información, se puede calcular la medida del cuarto lado y la otra diagonal.
4. ¿Es posible aplicar el teorema de Ptolomeo en cualquier cuadrilátero?
No, el teorema de Ptolomeo solo es aplicable en cuadriláteros cíclicos.
5. ¿Cuál es la fórmula del teorema de Ptolomeo?
La fórmula del teorema de Ptolomeo es a · c + b · d = e · f, donde a, b, c y d son los lados del cuadrilátero cíclico y e y f son las diagonales que se cruzan en el centro de la circunferencia que lo contiene.
Deja una respuesta