¡Resuelve tus dudas! Lógica proposicional: Ni P ni Q en 5 minutos

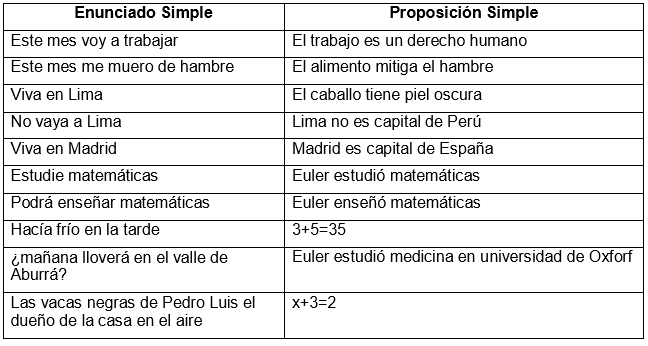
Si alguna vez te has enfrentado a un problema de lógica proposicional, es probable que hayas encontrado la expresión "Ni P ni Q". Esta es una de las tantas combinaciones lógicas que se pueden utilizar para construir argumentos válidos y razonamientos precisos. En este artículo, te explicaremos qué significa esta expresión y cómo puedes utilizarla para resolver problemas de lógica proposicional en solo 5 minutos.

¿Qué es la lógica proposicional?

Antes de entrar en detalle sobre la expresión "Ni P ni Q", es importante tener en cuenta qué es la lógica proposicional. En términos simples, la lógica proposicional es una rama de la lógica que se enfoca en el estudio de las proposiciones y sus relaciones lógicas. Una proposición es una afirmación que puede ser verdadera o falsa, como "El cielo es azul" o "2+2=5". La lógica proposicional se utiliza para analizar y evaluar la validez de los argumentos basados en proposiciones.

¿Qué significa "Ni P ni Q"?

La expresión "Ni P ni Q" se utiliza para expresar una negación conjunta de dos proposiciones, P y Q. En otras palabras, significa que ni P ni Q son verdaderas. Esta expresión se conoce como la negación de la disyunción, ya que es la negación de la afirmación "P o Q". La negación de la disyunción se representa en lógica proposicional como "~(P v Q)".

Ejemplo:

Imagina que tienes dos tazas de café, una con leche y otra sin leche. Si decimos que la taza con leche es P y la taza sin leche es Q, entonces la expresión "Ni P ni Q" significa que ninguna de las dos tazas tiene leche.

¿Cómo se utiliza "Ni P ni Q" en problemas de lógica proposicional?

La expresión "Ni P ni Q" puede utilizarse para construir argumentos válidos y razonamientos precisos. Por ejemplo, si queremos demostrar que algo no es cierto, podemos utilizar la negación de la disyunción para demostrar que ninguna de las opciones es válida.

Ejemplo:

Supongamos que tenemos dos puertas, una roja y una azul, y queremos demostrar que no hay un elefante detrás de ninguna de ellas. Si llamamos "P" a la proposición "Hay un elefante detrás de la puerta roja" y "Q" a la proposición "Hay un elefante detrás de la puerta azul", la expresión "Ni P ni Q" significa que no hay un elefante detrás de ninguna de las dos puertas.

Conclusión

La lógica proposicional es una herramienta útil para analizar y evaluar la validez de los argumentos basados en proposiciones. La expresión "Ni P ni Q" se utiliza para expresar una negación conjunta de dos proposiciones, P y Q. Esta expresión se puede utilizar para construir argumentos válidos y razonamientos precisos.

Preguntas frecuentes

1. ¿Qué es una proposición?

Una proposición es una afirmación que puede ser verdadera o falsa.

2. ¿Cómo se representa la negación de la disyunción en lógica proposicional?

La negación de la disyunción se representa como "~(P v Q)".

3. ¿Qué significa la expresión "Ni P ni Q"?

La expresión "Ni P ni Q" se utiliza para expresar una negación conjunta de dos proposiciones, P y Q.

4. ¿Cómo se puede utilizar la expresión "Ni P ni Q" en problemas de lógica proposicional?

La expresión "Ni P ni Q" se puede utilizar para construir argumentos válidos y razonamientos precisos.

5. ¿Por qué es importante la lógica proposicional?

La lógica proposicional es importante porque nos permite analizar y evaluar la validez de los argumentos basados en proposiciones, lo que nos ayuda a tomar decisiones informadas y a razonar de manera más precisa.