Resuelve conjuntos matemáticos fácilmente: guía práctica

Si eres estudiante de matemáticas, seguro has estudiado conjuntos. Los conjuntos son una parte fundamental de la matemática y se utilizan para organizar y clasificar objetos, números y conceptos. Sin embargo, resolver problemas de conjuntos puede ser complicado si no se tiene una buena comprensión de sus conceptos y propiedades. En este artículo, te presentaremos una guía práctica para resolver conjuntos matemáticos fácilmente.

1. Entendiendo los conjuntos

Los conjuntos se definen como una colección de objetos, números o conceptos que se agrupan juntos en una sola entidad. Los objetos que conforman un conjunto se llaman elementos. Por ejemplo, podemos tener un conjunto de números pares, que estaría conformado por los números 2, 4, 6, 8, etc.

2. Representación de conjuntos

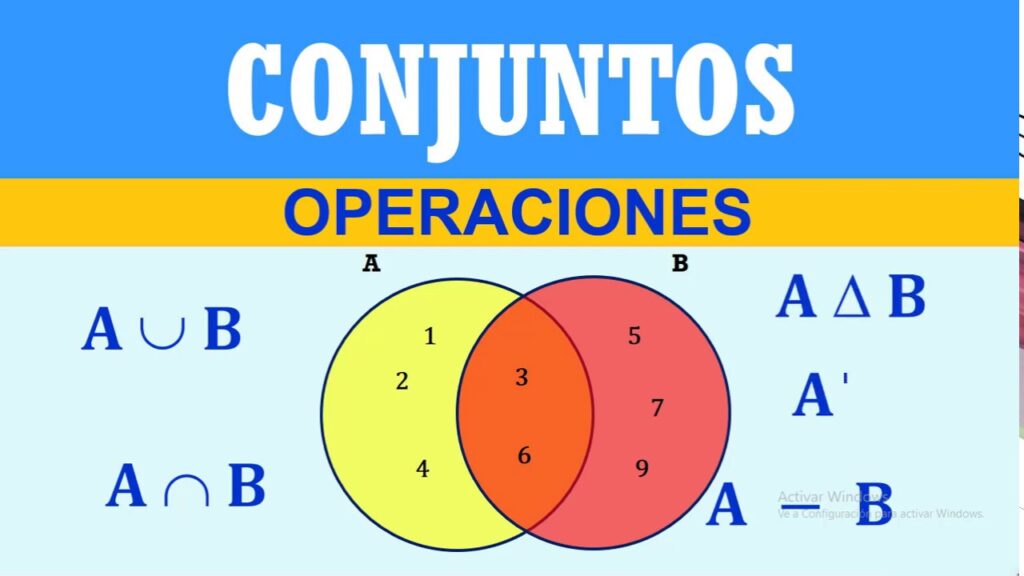
Los conjuntos se pueden representar de varias maneras. La forma más común es utilizando llaves {} para encerrar los elementos del conjunto. Por ejemplo, el conjunto de números pares se podría representar como {2, 4, 6, 8, ...}. También se pueden utilizar diagramas de Venn, donde se muestra la intersección y la unión de los conjuntos.

3. Operaciones con conjuntos

Existen varias operaciones que se pueden realizar con conjuntos:

Unión:

La unión de dos conjuntos A y B se representa como A ∪ B y está conformada por todos los elementos que pertenecen a A o a B o a ambos conjuntos. Por ejemplo, si A={1, 2, 3} y B={3, 4, 5}, la unión de A y B sería {1, 2, 3, 4, 5}.

Intersección:

La intersección de dos conjuntos A y B se representa como A ∩ B y está conformada por todos los elementos que pertenecen a ambos conjuntos. Por ejemplo, si A={1, 2, 3} y B={3, 4, 5}, la intersección de A y B sería {3}.

Diferencia:

La diferencia de dos conjuntos A y B se representa como A - B y está conformada por todos los elementos que pertenecen a A pero no a B. Por ejemplo, si A={1, 2, 3} y B={3, 4, 5}, la diferencia de A y B sería {1, 2}.

Complemento:

El complemento de un conjunto A se representa como A' y está conformada por todos los elementos que no pertenecen a A. Por ejemplo, si A={1, 2, 3}, el complemento de A sería todos los números que no son 1, 2 o 3.

4. Propiedades de los conjuntos

Existen varias propiedades de los conjuntos que se deben conocer para resolver problemas de conjuntos:

Propiedad conmutativa:

La propiedad conmutativa se refiere a que el orden de los conjuntos no afecta el resultado de la operación. Por ejemplo, A ∪ B es igual a B ∪ A.

Propiedad asociativa:

La propiedad asociativa se refiere a que la forma en que se agrupan los conjuntos en una operación no afecta el resultado final. Por ejemplo, (A ∪ B) ∪ C es igual a A ∪ (B ∪ C).

Propiedad distributiva:

La propiedad distributiva se refiere a que una operación se puede distribuir sobre otra operación. Por ejemplo, A ∩ (B ∪ C) es igual a (A ∩ B) ∪ (A ∩ C).

5. Ejemplos prácticos

Veamos algunos ejemplos prácticos para aplicar los conceptos y operaciones de conjuntos:

Ejemplo 1:

Si A={1, 2, 3, 4} y B={3, 4, 5, 6}, encuentra la unión, la intersección y la diferencia de A y B.

Solución:
La unión de A y B sería {1, 2, 3, 4, 5, 6}.
La intersección de A y B sería {3, 4}.
La diferencia de A y B sería {1, 2}.

Ejemplo 2:

Si A={1, 2, 3, 4} y B={3, 4, 5, 6}, encuentra el complemento de A.

Solución:
El complemento de A sería {5, 6}.

6. Conclusión

Resolver problemas de conjuntos puede ser complicado si no se tiene una buena comprensión de los conceptos y operaciones de conjuntos. En este artículo, hemos presentado una guía práctica para resolver conjuntos matemáticos fácilmente. Es importante tener en cuenta las propiedades de los conjuntos y cómo se pueden representar de diferentes maneras.

7. Preguntas frecuentes

¿Qué es un conjunto?

Un conjunto es una colección de objetos, números o conceptos que se agrupan juntos en una sola entidad.

¿Cómo se representan los conjuntos?

Los conjuntos se pueden representar utilizando llaves {} para encerrar los elementos del conjunto o mediante diagramas de Venn.

¿Cuáles son las operaciones con conjuntos?

Las operaciones con conjuntos son la unión, la intersección, la diferencia y el complemento.

¿Cuáles son las propiedades de los conjuntos?

Las propiedades de los conjuntos son la conmutativa, la asociativa y la distributiva.

¿Cómo se resuelven problemas de conjuntos?

Para resolver problemas de conjuntos, es importante comprender los conceptos y operaciones de conjuntos, y aplicar las propiedades de los conjuntos en los problemas.