Reglas de lógica difusa: una nueva perspectiva

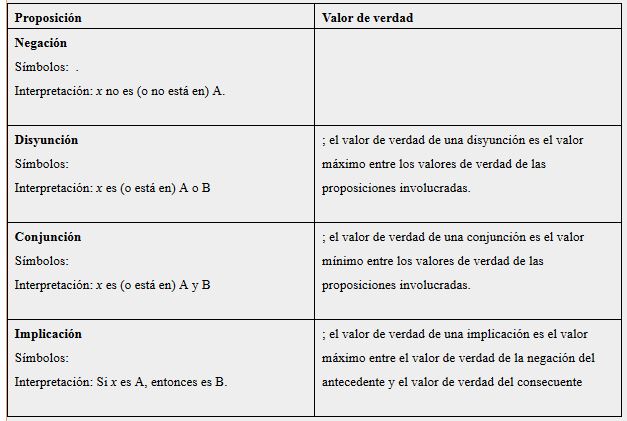
La lógica difusa es una teoría matemática que se utiliza para modelar situaciones en las que la verdad no es absoluta, sino que varía en grado. En la lógica difusa, las variables se representan mediante conjuntos difusos, que son conjuntos en los que los elementos tienen una pertenencia parcial. Esta teoría se utiliza en inteligencia artificial, robótica, sistemas de control, entre otros campos.

En este artículo, exploraremos las reglas de lógica difusa y cómo pueden proporcionar una nueva perspectiva en la toma de decisiones.

¿Qué son las reglas de lógica difusa?

Las reglas de lógica difusa son una forma de expresar el conocimiento en lógica difusa. Estas reglas se utilizan para relacionar las variables de entrada con las variables de salida en un sistema difuso. Una regla de lógica difusa se compone de dos partes: la antecedente y la consecuente.

La antecedente es una afirmación sobre las variables de entrada, expresada en términos de conjuntos difusos. Por ejemplo, "si la temperatura es alta" podría ser una antecedente.

La consecuente es una afirmación sobre la variable de salida, también expresada en términos de conjuntos difusos. Por ejemplo, "entonces el aire acondicionado debe estar encendido" podría ser una consecuente.

Cómo funcionan las reglas de lógica difusa

Las reglas de lógica difusa funcionan mediante la evaluación de la verdad de la antecedente y la consecuente en términos de conjuntos difusos. Para ello, se utilizan funciones de pertenencia para cada conjunto difuso.

Las funciones de pertenencia asignan un grado de pertenencia a cada elemento en el conjunto difuso. Por ejemplo, si el conjunto difuso es "temperatura alta", la función de pertenencia podría asignar un grado de pertenencia del 0.7 a una temperatura de 30 grados Celsius y un grado de pertenencia del 0.2 a una temperatura de 25 grados Celsius.

Una vez evaluadas las funciones de pertenencia de la antecedente y la consecuente, se utiliza un operador de inferencia para determinar el grado de verdad de la regla. El operador de inferencia combina los grados de pertenencia de la antecedente y la consecuente para obtener un grado de verdad para la regla.

Por qué las reglas de lógica difusa son importantes

Las reglas de lógica difusa son importantes porque permiten modelar situaciones en las que la verdad no es absoluta, sino que varía en grado. Esto es especialmente útil en situaciones en las que las variables no se pueden medir con precisión o en las que la interpretación humana es necesaria.

Por ejemplo, en un sistema de control de velocidad de un motor, la velocidad no se puede medir con precisión debido a la presencia de ruido en los sensores. En este caso, se pueden utilizar conjuntos difusos para modelar la velocidad y las reglas de lógica difusa para controlar la velocidad del motor.

Además, las reglas de lógica difusa también permiten la toma de decisiones basada en el conocimiento experto. Los expertos pueden expresar sus conocimientos en forma de reglas de lógica difusa, lo que permite la automatización de decisiones que normalmente requerirían la intervención humana.

Ejemplo de aplicación de las reglas de lógica difusa

Un ejemplo de aplicación de las reglas de lógica difusa es en un sistema de recomendación de películas. Supongamos que el sistema tiene dos variables de entrada: "calidad de la película" y "popularidad de la película", y una variable de salida: "recomendación de la película".

Las reglas de lógica difusa podrían expresarse de la siguiente manera:

- Si la calidad de la película es alta y la popularidad de la película es alta, entonces la recomendación de la película es "recomendada".
- Si la calidad de la película es baja y la popularidad de la película es alta, entonces la recomendación de la película es "posiblemente recomendada".
- Si la calidad de la película es alta y la popularidad de la película es baja, entonces la recomendación de la película es "posiblemente recomendada".
- Si la calidad de la película es baja y la popularidad de la película es baja, entonces la recomendación de la película es "no recomendada".

En este ejemplo, las funciones de pertenencia para las variables de entrada y salida se definirían de acuerdo a la interpretación de los expertos en cine.

Conclusión

Las reglas de lógica difusa proporcionan una nueva perspectiva en la toma de decisiones, permitiendo modelar situaciones en las que la verdad no es absoluta, sino que varía en grado. Esto es especialmente útil en situaciones en las que las variables no se pueden medir con precisión o en las que la interpretación humana es necesaria. Las reglas de lógica difusa también permiten la toma de decisiones basada en el conocimiento experto.

Preguntas frecuentes

¿Cuál es la diferencia entre la lógica difusa y la lógica clásica?

La lógica clásica se basa en la verdad absoluta, mientras que la lógica difusa permite la verdad en grado. En la lógica clásica, un enunciado es verdadero o falso, mientras que en la lógica difusa, un enunciado puede ser verdadero en un grado determinado.

¿Cuáles son las aplicaciones de la lógica difusa?

La lógica difusa se utiliza en inteligencia artificial, robótica, sistemas de control, sistemas de recomendación, entre otros campos.

¿Cómo se representan las variables en la lógica difusa?

En la lógica difusa, las variables se representan mediante conjuntos difusos, que son conjuntos en los que los elementos tienen una pertenencia parcial.

¿Qué son las funciones de pertenencia en la lógica difusa?

Las funciones de pertenencia asignan un grado de pertenencia a cada elemento en el conjunto difuso. Estas funciones se utilizan para evaluar la verdad de la antecedente y la consecuente en una regla de lógica difusa.

¿Cómo se evalúa la verdad de una regla de lógica difusa?

La verdad de una regla de lógica difusa se evalúa mediante el uso de un operador de inferencia, que combina los grados de pertenencia de la antecedente y la consecuente para obtener un grado de verdad para la regla.