Punto divisor de segmento: encuentra la razón exacta
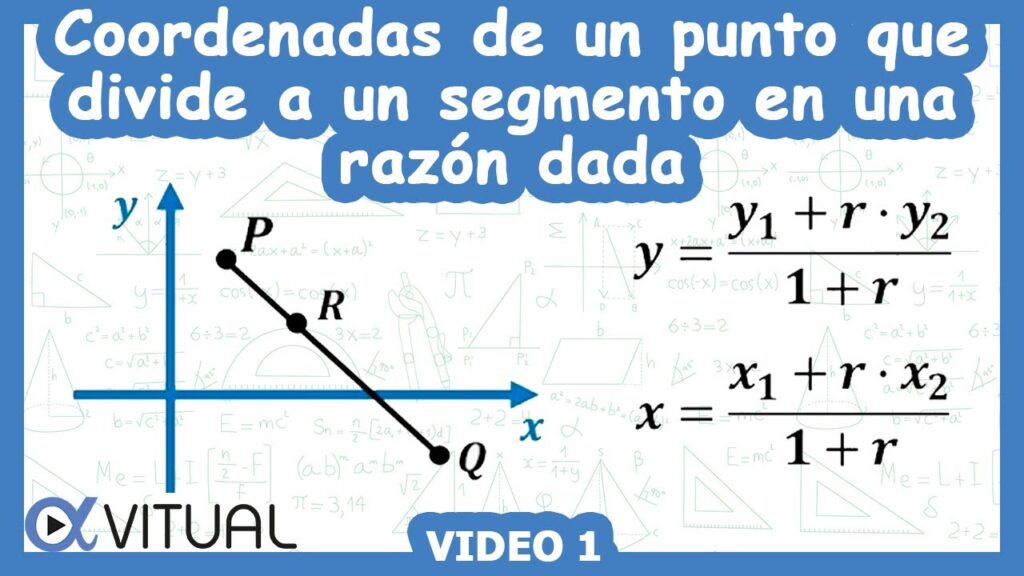
Cuando se trata de dividir un segmento en dos partes iguales, la solución es bastante simple: basta con encontrar el punto medio. Sin embargo, ¿qué sucede cuando necesitamos dividir un segmento en partes desiguales? En este caso, necesitamos encontrar el punto divisor de segmento, también conocido como punto de corte o punto de división. Este punto se encuentra en alguna parte del segmento, y divide el mismo en dos partes cuyas longitudes están en una proporción específica.
En este artículo, vamos a explicar cómo encontrar el punto divisor de segmento para cualquier proporción dada, utilizando una fórmula matemática simple. También vamos a explorar algunas aplicaciones prácticas de esta fórmula, y responder a algunas preguntas frecuentes sobre el tema. ¡Empecemos!
- ¿Qué es el punto divisor de segmento?
- ¿Cómo encontrar el punto divisor de segmento?
- Aplicaciones prácticas del punto divisor de segmento
-
Preguntas frecuentes
- ¿Puede un segmento ser dividido en una proporción irracional?
- ¿Es necesario conocer las coordenadas de los puntos A y B para encontrar el punto divisor de segmento?
- ¿Es posible que el punto divisor de segmento se encuentre fuera del segmento AB?
- ¿Qué sucede si la proporción en la que se desea dividir el segmento es mayor que 1?
- ¿Puedo utilizar el punto divisor de segmento para dividir un triángulo en dos partes iguales?
¿Qué es el punto divisor de segmento?
Antes de entrar en detalles sobre cómo encontrar el punto divisor de segmento, es importante entender qué es exactamente este punto. En términos simples, el punto divisor de segmento es un punto que se encuentra dentro de un segmento, y que divide el mismo en dos partes cuyas longitudes están en una proporción específica.
Por ejemplo, si queremos dividir un segmento AB en una proporción de 2:3, el punto divisor de segmento se encuentra en algún lugar entre A y B, de tal manera que la longitud de la parte AB que está más cerca de A es dos veces menor que la longitud de la parte AB que está más cerca de B.
¿Cómo encontrar el punto divisor de segmento?
Para encontrar el punto divisor de segmento, necesitamos conocer dos cosas: la proporción en la que deseamos dividir el segmento, y las coordenadas de los puntos A y B que delimitan el segmento.
Supongamos que queremos dividir el segmento AB en una proporción de m:n, donde m y n son números enteros positivos. Para encontrar el punto divisor de segmento, seguimos los siguientes pasos:
1. Calculamos la distancia total del segmento AB, utilizando la fórmula de la distancia entre dos puntos:
$$
d_{AB} = sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}
$$
Donde $x_A$, $y_A$, $x_B$ y $y_B$ son las coordenadas de los puntos A y B.
2. Calculamos la distancia desde A hasta el punto divisor de segmento, utilizando la fórmula:
$$
d_{AD} = frac{m}{m+n} times d_{AB}
$$
3. Usando la fórmula de la pendiente de una recta, encontramos las coordenadas del punto D:
$$
begin{aligned}
m_{AB} &= frac{y_B - y_A}{x_B - x_A} \
x_D &= x_A + frac{d_{AD}}{sqrt{1 + m_{AB}^2}} \
y_D &= y_A + m_{AB} times (x_D - x_A)
end{aligned}
$$
Donde $m_{AB}$ es la pendiente de la recta que pasa por los puntos A y B.
4. Verificamos que las longitudes de los segmentos AD y DB estén en la proporción deseada:
$$
begin{aligned}
frac{AD}{DB} &= frac{m}{n} \
frac{d_{AD}}{d_{AB} - d_{AD}} &= frac{m}{n}
end{aligned}
$$
Si la proporción es correcta, entonces el punto D es el punto divisor de segmento buscado.
Aplicaciones prácticas del punto divisor de segmento
El punto divisor de segmento tiene muchas aplicaciones prácticas en la geometría y en otras áreas de la ciencia y la ingeniería. Algunas de las aplicaciones más comunes incluyen:
- Diseño de estructuras: En el diseño de estructuras, el punto divisor de segmento se utiliza para encontrar el centro de gravedad de un objeto. El centro de gravedad es el punto en el que la masa de un objeto está equilibrada, y se puede encontrar dividiendo el objeto en segmentos y encontrando el punto divisor de cada uno de ellos.
- Óptica: En la óptica, el punto divisor de segmento se utiliza para encontrar el punto de enfoque de una lente. El punto de enfoque es el punto en el que los rayos de luz paralelos se cruzan después de pasar a través de la lente, y se puede encontrar dividiendo la distancia focal de la lente en una proporción específica.
- Análisis de datos: En el análisis de datos, el punto divisor de segmento se utiliza para encontrar el percentil de una distribución. El percentil es el valor por debajo del cual cae una cierta proporción de los datos, y se puede encontrar dividiendo los datos en segmentos y encontrando el punto divisor de cada uno de ellos.
Preguntas frecuentes
¿Puede un segmento ser dividido en una proporción irracional?
Sí, un segmento puede ser dividido en una proporción irracional. En este caso, el punto divisor de segmento no puede ser expresado exactamente en términos de las coordenadas de los puntos A y B, pero se puede encontrar con una precisión arbitraria utilizando una aproximación numérica.
¿Es necesario conocer las coordenadas de los puntos A y B para encontrar el punto divisor de segmento?
Sí, es necesario conocer las coordenadas de los puntos A y B para encontrar el punto divisor de segmento. Sin embargo, en algunos casos, como en el diseño de estructuras o en la óptica, estas coordenadas pueden ser conocidas a priori.
¿Es posible que el punto divisor de segmento se encuentre fuera del segmento AB?
No, el punto divisor de segmento siempre se encuentra dentro del segmento AB. Si el punto divisor de segmento se encuentra fuera del segmento, entonces la proporción en la que se divide el segmento no es válida.
¿Qué sucede si la proporción en la que se desea dividir el segmento es mayor que 1?
Si la proporción en la que se desea dividir el segmento es mayor que 1, entonces el punto divisor de segmento se encuentra en la extensión del segmento AB más allá del punto B. En este caso, las coordenadas del punto divisor de segmento pueden ser encontradas utilizando la misma fórmula que se utiliza para encontrar el punto dentro del segmento.
¿Puedo utilizar el punto divisor de segmento para dividir un triángulo en dos partes iguales?
No, el punto divisor de segmento sólo se puede utilizar para dividir un segmento en partes desiguales en una proporción específica. Para dividir un triángulo en dos partes iguales, es necesario encontrar el punto de equidistancia, que es el punto que se encuentra a la misma distancia de los tres vértices del triángulo.
Deja una respuesta