Prueba del axioma de elección: método y aplicaciones

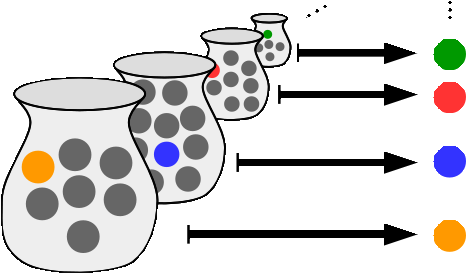
El axioma de elección es uno de los postulados fundamentales de la teoría de conjuntos. Este afirma que, dada una colección de conjuntos no vacíos, es posible elegir un elemento de cada uno de ellos. Aunque este axioma es muy útil en muchas áreas de las matemáticas, su inclusión en la teoría de conjuntos ha sido objeto de cierta controversia. Por esta razón, se ha buscado demostrar su veracidad de manera rigurosa. En este artículo, explicaremos el método usado para demostrar el axioma de elección y sus aplicaciones.

La prueba del axioma de elección

La prueba del axioma de elección se basa en el concepto de función de elección. Una función de elección es una función que, dada una colección de conjuntos no vacíos, elige un elemento de cada uno de ellos. Es importante notar que, aunque es intuitivamente claro que puede existir una función de elección para cualquier colección de conjuntos no vacíos, la existencia de una función de elección para cualquier colección de conjuntos no vacíos no es trivial.

La prueba del axioma de elección se basa en la demostración de que, para cualquier colección de conjuntos no vacíos, existe una función de elección. Para ello, se utiliza el teorema de Zorn, que afirma que toda cadena en un conjunto parcialmente ordenado no vacío tiene un límite superior. Este teorema se aplica a una colección de conjuntos con una relación de inclusión parcialmente ordenada. La aplicación del teorema de Zorn permite demostrar que existe un conjunto maximal de conjuntos disjuntos, lo que a su vez permite demostrar la existencia de una función de elección para cualquier colección de conjuntos no vacíos.

Aplicaciones del axioma de elección

El axioma de elección tiene muchas aplicaciones en las matemáticas y en otras áreas, como la física y la informática. Algunas de las aplicaciones más importantes son las siguientes:

Geometría y topología

El axioma de elección se utiliza en la demostración de varios resultados importantes en geometría y topología, como el teorema de Tychonoff y el teorema de Hahn-Banach. El teorema de Tychonoff afirma que un producto arbitrario de espacios compactos es compacto. El teorema de Hahn-Banach es un resultado fundamental en la teoría de las funciones lineales continuas en espacios vectoriales normados.

Análisis

El axioma de elección también se utiliza en varios resultados importantes en análisis, como el teorema de Banach-Steinhaus y el teorema de Carathéodory. El teorema de Banach-Steinhaus es un resultado fundamental en la teoría de los operadores lineales continuos. El teorema de Carathéodory es un resultado importante en la teoría de la medida.

Teoría de juegos

El axioma de elección se utiliza en la teoría de juegos para demostrar la existencia de estrategias óptimas en ciertos juegos. Por ejemplo, se utiliza en la demostración del teorema de von Neumann sobre la existencia de una estrategia óptima en juegos de suma cero.

Preguntas frecuentes

¿Qué es el axioma de elección?

El axioma de elección es uno de los postulados fundamentales de la teoría de conjuntos. Este afirma que, dada una colección de conjuntos no vacíos, es posible elegir un elemento de cada uno de ellos.

¿Por qué el axioma de elección es importante en las matemáticas?

El axioma de elección es importante en las matemáticas porque tiene muchas aplicaciones en diferentes áreas, como la geometría, la topología, el análisis y la teoría de juegos.

¿Por qué el axioma de elección ha sido objeto de controversia?

El axioma de elección ha sido objeto de controversia porque su inclusión en la teoría de conjuntos ha llevado a algunas paradojas, como la paradoja de Banach-Tarski, que afirma que es posible descomponer una esfera en un número finito de piezas y reensamblarlas para obtener dos esferas idénticas a la original.

¿Es posible demostrar el axioma de elección sin utilizar el teorema de Zorn?

No se conoce ninguna demostración del axioma de elección que no utilice el teorema de Zorn o algún principio equivalente.

¿Por qué es importante demostrar el axioma de elección?

Demostrar el axioma de elección es importante porque garantiza la existencia de una función de elección para cualquier colección de conjuntos no vacíos, lo que permite demostrar muchos resultados importantes en diferentes áreas de las matemáticas y otras disciplinas relacionadas.