Proposiciones lógicas: representación matemática
Las proposiciones lógicas son una herramienta fundamental en el campo de la lógica matemática y la informática, ya que permiten expresar afirmaciones de manera precisa y formal. En este artículo, vamos a hablar sobre la representación matemática de las proposiciones lógicas y su importancia en la resolución de problemas.
- ¿Qué son las proposiciones lógicas?
- Representación matemática de las proposiciones lógicas
- Tabla de verdad
- Importancia en la resolución de problemas
- Conclusión
-
Preguntas frecuentes
- ¿Cómo se representan las proposiciones lógicas?
- ¿Qué es una tabla de verdad?
- ¿Por qué son importantes las proposiciones lógicas en la resolución de problemas?
- ¿Cómo se utilizan las proposiciones lógicas en la programación?
- ¿Qué es la implicación en la representación matemática de las proposiciones lógicas?
¿Qué son las proposiciones lógicas?
Antes de entrar en detalle sobre su representación, es importante entender qué son las proposiciones lógicas. En términos simples, una proposición lógica es una afirmación que puede ser verdadera o falsa. Por ejemplo, "el cielo es azul" es una proposición lógica que puede ser verdadera o falsa dependiendo de las condiciones climáticas.
Las proposiciones lógicas se utilizan para expresar ideas, definir conceptos y construir argumentos. En el campo de la lógica matemática y la informática, las proposiciones lógicas se utilizan para la construcción de algoritmos y la resolución de problemas.
Representación matemática de las proposiciones lógicas
Las proposiciones lógicas se representan matemáticamente utilizando variables y operadores lógicos. Las variables representan los elementos que se están analizando en la proposición, mientras que los operadores lógicos se utilizan para conectar las variables y construir la afirmación lógica.
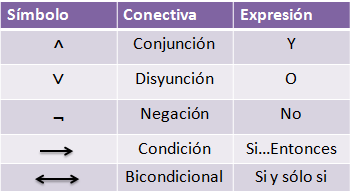
Los operadores lógicos más comunes son la conjunción, la disyunción, la negación y la implicación. La conjunción se utiliza para unir dos proposiciones y se representa con el símbolo ∧ (y). La disyunción se utiliza para unir dos proposiciones con el objetivo de que al menos una de ellas sea verdadera y se representa con el símbolo ∨ (o). La negación se utiliza para negar una proposición y se representa con el símbolo ¬ (no). La implicación se utiliza para expresar la relación entre dos proposiciones y se representa con el símbolo → (si...entonces).
Por ejemplo, si queremos expresar la proposición "Si llueve, entonces me quedo en casa", podemos representarla matemáticamente como "p → q", donde p es la proposición "llueve" y q es la proposición "me quedo en casa".
Tabla de verdad
Una tabla de verdad es una herramienta utilizada para determinar la verdad o falsedad de una proposición lógica. En una tabla de verdad, se analizan todas las posibles combinaciones de valores de verdad de las variables involucradas en la proposición.
Por ejemplo, si queremos analizar la proposición "p ∧ q", donde p es verdadero y q es falso, podemos construir una tabla de verdad de la siguiente manera:
| p | q | p ∧ q |
| - | - | ----- |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
En este caso, la proposición "p ∧ q" es verdadera solo cuando ambas variables son verdaderas.
Importancia en la resolución de problemas
La representación matemática de las proposiciones lógicas es fundamental en la resolución de problemas, ya que permite construir algoritmos y sistemas de decisión basados en la lógica.
Por ejemplo, en la programación, las proposiciones lógicas se utilizan para construir estructuras de control de flujo, como los condicionales y los bucles. En el análisis de datos, las proposiciones lógicas se utilizan para definir criterios de selección y filtrado de información.
Conclusión
Las proposiciones lógicas son una herramienta fundamental en la lógica matemática y la informática. Su representación matemática permite expresar afirmaciones de manera precisa y formal, y su importancia en la resolución de problemas es innegable.
Preguntas frecuentes
¿Cómo se representan las proposiciones lógicas?
Las proposiciones lógicas se representan matemáticamente utilizando variables y operadores lógicos, como la conjunción, la disyunción, la negación y la implicación.
¿Qué es una tabla de verdad?
Una tabla de verdad es una herramienta utilizada para determinar la verdad o falsedad de una proposición lógica. En una tabla de verdad, se analizan todas las posibles combinaciones de valores de verdad de las variables involucradas en la proposición.
¿Por qué son importantes las proposiciones lógicas en la resolución de problemas?
Las proposiciones lógicas son importantes en la resolución de problemas porque permiten construir algoritmos y sistemas de decisión basados en la lógica, lo que facilita la automatización de procesos y la toma de decisiones.
¿Cómo se utilizan las proposiciones lógicas en la programación?
En la programación, las proposiciones lógicas se utilizan para construir estructuras de control de flujo, como los condicionales y los bucles. También se utilizan para definir criterios de selección y filtrado de información.
¿Qué es la implicación en la representación matemática de las proposiciones lógicas?
La implicación es un operador lógico que se utiliza para expresar la relación entre dos proposiciones. Se representa con el símbolo → (si...entonces) y se utiliza para expresar que la proposición a implica la proposición b.
Deja una respuesta