Postulados de la lógica booleana: ¡Descubre cómo funciona!
La lógica booleana es una rama de la matemática que se encarga de estudiar el comportamiento de las operaciones lógicas sobre proposiciones. Esta disciplina fue desarrollada por el matemático inglés George Boole en el siglo XIX y ha sido fundamental en la creación de los sistemas digitales que utilizamos hoy en día. En este artículo, te explicaremos los postulados de la lógica booleana y cómo funcionan.
¿Qué es la lógica booleana?
La lógica booleana se basa en el uso de dos valores: verdadero (V) y falso (F). Estos valores se utilizan para representar proposiciones que pueden ser verdaderas o falsas. Por ejemplo, la proposición "el cielo es azul" puede ser verdadera o falsa, dependiendo del momento del día y de las condiciones meteorológicas.
Para trabajar con proposiciones, la lógica booleana utiliza tres operaciones fundamentales:
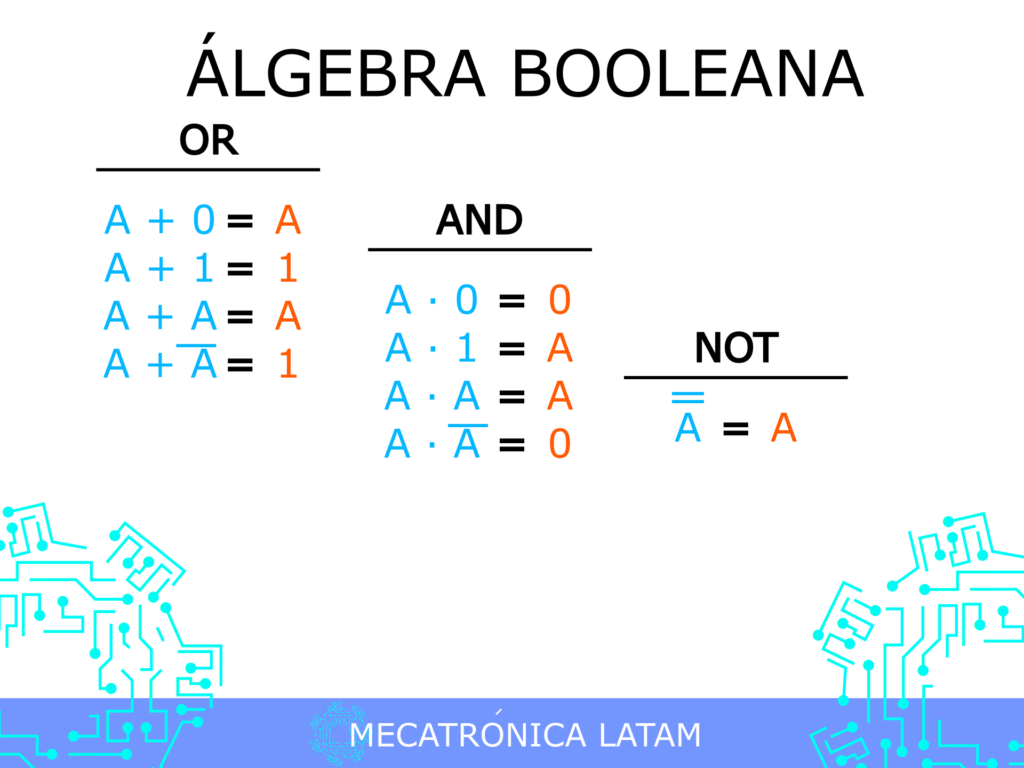
- Negación (¬): esta operación cambia el valor de la proposición. Si la proposición es verdadera, la negación la convierte en falsa, y viceversa. Por ejemplo, la negación de la proposición "el cielo es azul" es "el cielo no es azul".
- Conjunción (∧): esta operación se utiliza para combinar dos o más proposiciones en una sola. La proposición resultante es verdadera si todas las proposiciones originales son verdaderas. Por ejemplo, la conjunción de las proposiciones "el cielo es azul" y "hace sol" es "el cielo es azul y hace sol".
- Disyunción (∨): esta operación se utiliza para combinar dos o más proposiciones en una sola. La proposición resultante es verdadera si al menos una de las proposiciones originales es verdadera. Por ejemplo, la disyunción de las proposiciones "el cielo es azul" y "está nublado" es "el cielo es azul o está nublado".
Postulados de la lógica booleana
Los postulados de la lógica booleana son principios que se utilizan para trabajar con proposiciones y operaciones lógicas. Estos postulados son:
- Identidad: la conjunción de una proposición con la proposición verdadera es igual a la proposición original. Por ejemplo, "el cielo es azul y verdadero" es igual a "el cielo es azul".
- Negación: la conjunción de una proposición con su negación es igual a la proposición falsa. Por ejemplo, "el cielo es azul y el cielo no es azul" es igual a "falso".
- Conmutatividad: el orden de las proposiciones en una conjunción o disyunción no afecta al resultado. Por ejemplo, "el cielo es azul y hace sol" es igual a "hace sol y el cielo es azul".
- Asociatividad: el agrupamiento de las proposiciones en una conjunción o disyunción no afecta al resultado. Por ejemplo, "(el cielo es azul y hace sol) y está despejado" es igual a "el cielo es azul y (hace sol y está despejado)".
- Distributividad: la conjunción o disyunción de una proposición con la conjunción o disyunción de otra proposición es igual a la conjunción o disyunción de las proposiciones individuales. Por ejemplo, "el cielo es azul y (hace sol o está despejado)" es igual a "(el cielo es azul y hace sol) o (el cielo es azul y está despejado)".
- Leyes de De Morgan: la negación de una conjunción o disyunción es igual a la disyunción o conjunción de las negaciones individuales. Por ejemplo, "no (el cielo es azul y hace sol)" es igual a "no el cielo es azul o no hace sol".
Aplicaciones de la lógica booleana
La lógica booleana tiene aplicaciones en diversos campos, como la informática, la electrónica y la ingeniería. En informática, por ejemplo, se utiliza para el diseño de circuitos digitales y para la programación. Los lenguajes de programación utilizan operaciones booleanas para evaluar condiciones y controlar el flujo de ejecución de un programa.
En electrónica, la lógica booleana se utiliza para el diseño de circuitos digitales. Los circuitos digitales utilizan señales eléctricas que pueden tener dos estados: encendido (1) o apagado (0). Las operaciones booleanas se utilizan para combinar y manipular estas señales y así realizar operaciones lógicas complejas.
Conclusión
La lógica booleana es una herramienta fundamental en la matemática y tiene aplicaciones en diversos campos. Los postulados de la lógica booleana son principios que se utilizan para trabajar con proposiciones y operaciones lógicas. Conocer estos postulados es esencial para entender cómo funcionan los sistemas digitales y cómo se pueden diseñar y programar.
Preguntas frecuentes
¿Qué es una proposición?
Una proposición es una afirmación que puede ser verdadera o falsa. Por ejemplo, "el cielo es azul" es una proposición.
¿Qué es la negación?
La negación es una operación lógica que cambia el valor de una proposición. Si la proposición es verdadera, la negación la convierte en falsa, y viceversa.
¿Cómo se utiliza la lógica booleana en la programación?
En la programación, la lógica booleana se utiliza para evaluar condiciones y controlar el flujo de ejecución de un programa. Los lenguajes de programación utilizan operaciones booleanas como "if" y "while" para realizar estas tareas.
¿Qué es un circuito digital?
Un circuito digital es un circuito electrónico que utiliza señales eléctricas que pueden tener dos estados: encendido (1) o apagado (0). Estos circuitos se utilizan en la electrónica y la informática para realizar operaciones lógicas y almacenar información.
¿Qué es la conjunción?
La conjunción es una operación lógica que se utiliza para combinar dos o más proposiciones en una sola. La proposición resultante es verdadera si todas las proposiciones originales son verdaderas.
Deja una respuesta