Lógica proposicional: simplifica la complejidad del lenguaje natural

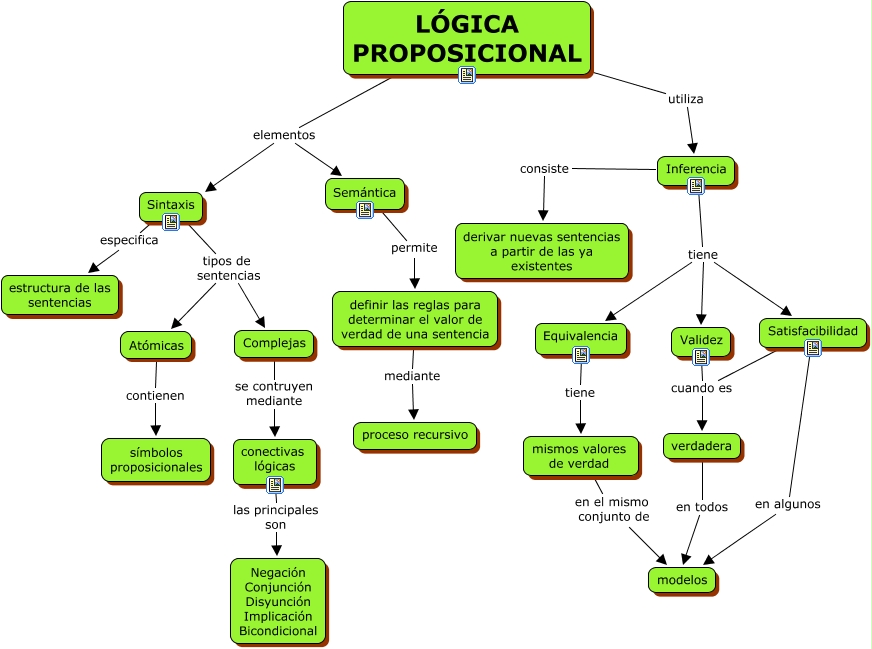
La lógica proposicional es un campo de la lógica que se encarga del estudio de las proposiciones, es decir, afirmaciones o negaciones que pueden ser verdaderas o falsas. Esta rama de la lógica se utiliza para simplificar la complejidad del lenguaje natural y hacerlo más fácil de entender.

En este artículo, exploraremos cómo la lógica proposicional puede ayudarnos a entender mejor el lenguaje natural. Comenzaremos por definir qué es la lógica proposicional y cómo funciona. Luego, veremos cómo se puede aplicar en diferentes contextos para simplificar la comunicación.

¿Qué es la lógica proposicional?

La lógica proposicional es una rama de la lógica que se encarga de estudiar las proposiciones. Una proposición es una afirmación o negación que puede ser verdadera o falsa. Por ejemplo, "el cielo es azul" es una proposición que puede ser verdadera o falsa, dependiendo del momento del día y las condiciones climáticas.

La lógica proposicional utiliza símbolos para representar proposiciones y operadores lógicos para combinarlas. Los símbolos más comunes son las letras minúsculas del alfabeto, como p, q, r, s, etc. Los operadores lógicos más comunes son la negación (~), la conjunción (^), la disyunción (v) y la implicación (→).

¿Cómo funciona la lógica proposicional?

La lógica proposicional funciona mediante la combinación de proposiciones utilizando los operadores lógicos. A continuación, se explican brevemente los cuatro operadores lógicos más comunes:

- Negación (~): este operador se utiliza para negar una proposición. Por ejemplo, si la proposición es "el cielo es azul", su negación sería "~el cielo es azul", que significa "el cielo no es azul".

- Conjunción (^): este operador se utiliza para combinar dos proposiciones en una sola proposición. Por ejemplo, si las proposiciones son "el cielo es azul" y "el sol está brillando", su conjunción sería "el cielo es azul ^ el sol está brillando", que significa "el cielo es azul y el sol está brillando".

- Disyunción (v): este operador se utiliza para combinar dos proposiciones en una sola proposición. Por ejemplo, si las proposiciones son "el cielo es azul" y "está lloviendo", su disyunción sería "el cielo es azul v está lloviendo", que significa "el cielo es azul o está lloviendo".

- Implicación (→): este operador se utiliza para expresar una relación de causa y efecto entre dos proposiciones. Por ejemplo, si la proposición es "si llueve, me quedo en casa", su implicación sería "llueve → me quedo en casa", que significa "si llueve, entonces me quedo en casa".

¿Cómo se aplica la lógica proposicional en diferentes contextos?

La lógica proposicional se puede aplicar en diferentes contextos para simplificar la comunicación y hacerla más clara y precisa. A continuación, se mencionan algunos ejemplos:

- En matemáticas: la lógica proposicional se utiliza para demostrar teoremas y resolver problemas matemáticos. Por ejemplo, en geometría, se pueden utilizar proposiciones y operadores lógicos para demostrar que dos triángulos son congruentes.

- En informática: la lógica proposicional se utiliza en la programación para diseñar algoritmos y desarrollar sistemas de software. Por ejemplo, se pueden utilizar proposiciones y operadores lógicos para crear condicionales y bucles en un programa.

- En filosofía: la lógica proposicional se utiliza para analizar y evaluar argumentos y teorías filosóficas. Por ejemplo, se pueden utilizar proposiciones y operadores lógicos para demostrar que una teoría es consistente o inconsistente.

- En derecho: la lógica proposicional se utiliza en la argumentación jurídica para analizar y evaluar las pruebas y las conclusiones de un caso. Por ejemplo, se pueden utilizar proposiciones y operadores lógicos para demostrar que una prueba es concluyente o insuficiente.

Conclusión

La lógica proposicional es una herramienta valiosa para simplificar la complejidad del lenguaje natural y hacerlo más fácil de entender. Esta rama de la lógica utiliza símbolos y operadores lógicos para representar y combinar proposiciones, lo que permite analizar y evaluar argumentos y teorías en diferentes contextos, desde las matemáticas hasta el derecho. Si quieres mejorar tu capacidad de comunicación y análisis, aprender lógica proposicional puede ser una buena opción.

Preguntas frecuentes

1. ¿Qué es una proposición?

Una proposición es una afirmación o negación que puede ser verdadera o falsa.

2. ¿Qué son los operadores lógicos?

Los operadores lógicos son símbolos que se utilizan para combinar proposiciones en la lógica proposicional. Los operadores más comunes son la negación (~), la conjunción (^), la disyunción (v) y la implicación (→).

3. ¿Qué es la negación?

La negación es un operador lógico que se utiliza para negar una proposición. Por ejemplo, si la proposición es "el cielo es azul", su negación sería "~el cielo es azul", que significa "el cielo no es azul".

4. ¿Qué es la implicación?

La implicación es un operador lógico que se utiliza para expresar una relación de causa y efecto entre dos proposiciones. Por ejemplo, si la proposición es "si llueve, me quedo en casa", su implicación sería "llueve → me quedo en casa", que significa "si llueve, entonces me quedo en casa".

5. ¿En qué contextos se aplica la lógica proposicional?

La lógica proposicional se aplica en diferentes contextos, desde las matemáticas hasta el derecho. Se utiliza para demostrar teoremas y resolver problemas matemáticos, diseñar algoritmos y desarrollar sistemas de software en informática, analizar y evaluar argumentos y teorías filosóficas, y analizar y evaluar las pruebas y las conclusiones de un caso en derecho.