Lógica matemática: ejemplos y definición clara

La lógica matemática es una rama de las matemáticas que se enfoca en el estudio de la estructura y el razonamiento lógico. Es una herramienta fundamental tanto en la matemática como en otras áreas, como la filosofía, la informática y la inteligencia artificial.

Para entender la lógica matemática, es importante comenzar por definir algunos conceptos clave. En primer lugar, tenemos las proposiciones, que son afirmaciones que pueden ser verdaderas o falsas. Por ejemplo, "2+2=4" es una proposición verdadera, mientras que "el cielo es verde" es una proposición falsa.

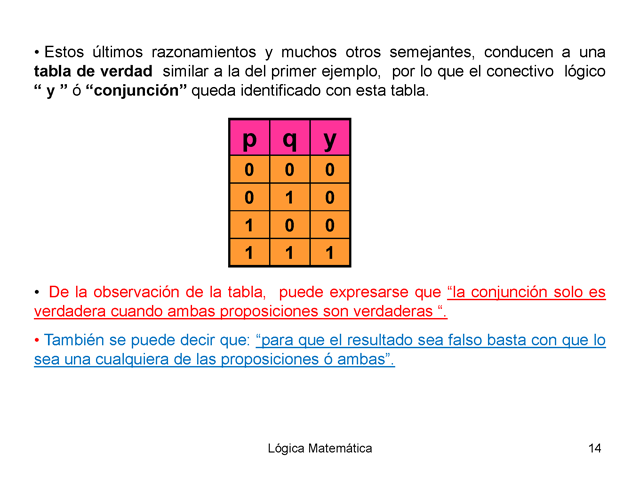
Además de las proposiciones, tenemos los conectores lógicos, que son palabras que se usan para combinar proposiciones. Algunos ejemplos de conectores lógicos son "y", "o" y "no". Por ejemplo, si tenemos las proposiciones "A" y "B", podemos combinarlas usando el conector lógico "y" para formar la proposición "A y B".

Otro concepto importante en la lógica matemática es el de la implicación. La implicación es una relación entre dos proposiciones, en la que una proposición (llamada antecedente) implica la otra (llamada consecuente). La implicación se denota por la flecha "->". Por ejemplo, la proposición "Si A entonces B" se puede escribir como "A -> B".

Ahora que hemos definido algunos conceptos clave, podemos ver algunos ejemplos de cómo se aplica la lógica matemática en la vida cotidiana. Un ejemplo común es el del razonamiento deductivo. Supongamos que tenemos las proposiciones "Todos los perros tienen cuatro patas" y "Fido es un perro". Podemos usar la implicación para deducir que "Fido tiene cuatro patas".

Otro ejemplo es el del razonamiento inductivo. Supongamos que observamos que todos los días, a las 12 del mediodía, el sol se encuentra en el cielo. Podemos usar la lógica matemática para inferir que el sol estará en el cielo mañana al mediodía.

En la informática y la inteligencia artificial, la lógica matemática se utiliza para el diseño de algoritmos y sistemas de razonamiento automatizado. Por ejemplo, los sistemas de inteligencia artificial pueden usar la lógica matemática para tomar decisiones basadas en conjuntos de reglas y datos.

La lógica matemática es una herramienta fundamental en la matemática y en otras áreas, como la filosofía, la informática y la inteligencia artificial. Al entender los conceptos clave, como las proposiciones, los conectores lógicos y la implicación, podemos aplicar la lógica matemática en la vida cotidiana y en el diseño de sistemas automatizados.

Ejemplos de proposiciones y conectores lógicos

- Proposición: "La tierra es redonda".
- Proposición: "El agua hierve a 100 grados Celsius".
- Proposición: "El cielo es azul".
- Conector lógico "y": "El agua es líquida y fluye".
- Conector lógico "o": "El examen es mañana o el próximo martes".
- Conector lógico "no": "No llueve hoy".

La implicación en la lógica matemática

La implicación es una relación entre dos proposiciones, en la que una proposición (llamada antecedente) implica la otra (llamada consecuente). La implicación se denota por la flecha "->". Por ejemplo, la proposición "Si A entonces B" se puede escribir como "A -> B".

- Proposición: "Si llueve, me llevaré un paraguas".
- Proposición: "Si estudio, aprobaré el examen".
- Proposición: "Si como mucho, me sentiré mal".
- Implicación: "Si llueve -> me llevaré un paraguas".
- Implicación: "Si estudio -> aprobaré el examen".
- Implicación: "Si como mucho -> me sentiré mal".

Aplicaciones de la lógica matemática

La lógica matemática se utiliza en una variedad de campos, como la matemática, la filosofía, la informática y la inteligencia artificial.

- En matemáticas, la lógica matemática se utiliza para demostrar teoremas y establecer relaciones entre diferentes conceptos matemáticos.
- En filosofía, la lógica matemática se utiliza para analizar argumentos y establecer la validez de las conclusiones.
- En informática, la lógica matemática se utiliza para el diseño de algoritmos y sistemas de razonamiento automatizado.
- En inteligencia artificial, la lógica matemática se utiliza para el diseño de sistemas de toma de decisiones basados en reglas y datos.

Preguntas frecuentes

¿Qué es la lógica matemática?

La lógica matemática es una rama de las matemáticas que se enfoca en el estudio de la estructura y el razonamiento lógico.

¿Qué son las proposiciones en la lógica matemática?

Las proposiciones son afirmaciones que pueden ser verdaderas o falsas.

¿Qué son los conectores lógicos?

Los conectores lógicos son palabras que se usan para combinar proposiciones. Algunos ejemplos de conectores lógicos son "y", "o" y "no".

¿Para qué se utiliza la implicación en la lógica matemática?

La implicación se utiliza para establecer una relación entre dos proposiciones, en la que una proposición implica la otra.

¿En qué campos se utiliza la lógica matemática?

La lógica matemática se utiliza en una variedad de campos, como la matemática, la filosofía, la informática y la inteligencia artificial.