Lenguaje formal para la lógica matemática: guía esencial

La lógica matemática es una rama de las matemáticas que se enfoca en la argumentación y el razonamiento lógico. En este campo, el lenguaje formal es esencial para poder expresar de manera precisa y rigurosa las ideas y conceptos.

En este artículo, te ofrecemos una guía esencial sobre el lenguaje formal para la lógica matemática, que te ayudará a comprender mejor esta disciplina y a comunicarte de manera efectiva en ella.

¿Qué es el lenguaje formal?

El lenguaje formal es un sistema de símbolos y reglas que se utiliza para expresar ideas y conceptos de manera precisa y rigurosa. En la lógica matemática, el lenguaje formal se utiliza para expresar las proposiciones y los argumentos de manera clara y sin ambigüedades.

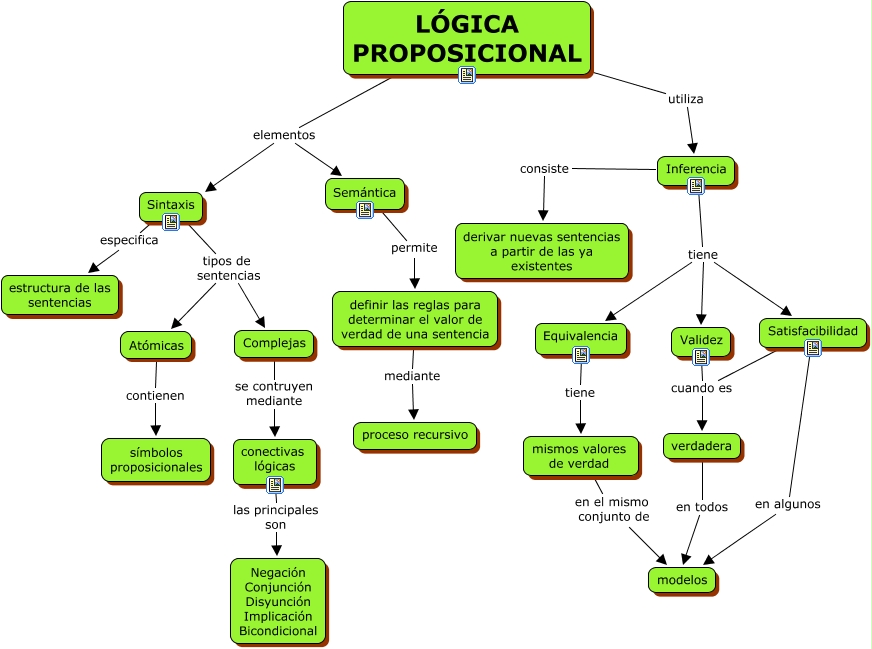
Proposiciones y conectivas lógicas

En la lógica matemática, una proposición es una afirmación que puede ser verdadera o falsa. Por ejemplo, "5 es un número par" es una proposición, que es verdadera, mientras que "2 + 2 = 5" es otra proposición, que es falsa.

Las conectivas lógicas son símbolos que se utilizan para conectar proposiciones y formar nuevas proposiciones. Las principales conectivas lógicas son la negación, la conjunción, la disyunción, la implicación y la equivalencia.

La negación se denota por el símbolo ¬ y se utiliza para formar la proposición contraria a una proposición dada. Por ejemplo, si p es la proposición "5 es un número par", entonces ¬p es la proposición "5 no es un número par".

La conjunción se denota por el símbolo ∧ y se utiliza para formar la proposición que es verdadera si y solo si ambas proposiciones que conecta son verdaderas. Por ejemplo, si p es la proposición "5 es un número par" y q es la proposición "7 es un número impar", entonces p ∧ q es la proposición "5 es un número par y 7 es un número impar".

La disyunción se denota por el símbolo ∨ y se utiliza para formar la proposición que es verdadera si al menos una de las proposiciones que conecta es verdadera. Por ejemplo, si p es la proposición "5 es un número par" y q es la proposición "7 es un número impar", entonces p ∨ q es la proposición "5 es un número par o 7 es un número impar".

La implicación se denota por el símbolo → y se utiliza para formar la proposición que es falsa solo cuando la proposición antecedente es verdadera y la proposición consecuente es falsa. Por ejemplo, si p es la proposición "5 es un número par" y q es la proposición "10 es un número par", entonces p → q es la proposición "Si 5 es un número par, entonces 10 es un número par".

La equivalencia se denota por el símbolo ↔ y se utiliza para formar la proposición que es verdadera cuando ambas proposiciones que conecta tienen el mismo valor de verdad. Por ejemplo, si p es la proposición "5 es un número par" y q es la proposición "10 es un número par", entonces p ↔ q es la proposición "5 y 10 son números pares".

Variables y cuantificadores

En la lógica matemática, las variables se utilizan para representar objetos o elementos de un conjunto. Por ejemplo, x puede representar un número real cualquiera.

Los cuantificadores se utilizan para expresar la cantidad de elementos de un conjunto que satisfacen una propiedad dada. Los principales cuantificadores son el cuantificador universal (∀) y el cuantificador existencial (∃).

El cuantificador universal se utiliza para afirmar que una propiedad es verdadera para todos los elementos de un conjunto. Por ejemplo, si P(x) es la propiedad "x es un número par", entonces ∀x P(x) es la proposición "Todos los números son pares".

El cuantificador existencial se utiliza para afirmar que al menos un elemento de un conjunto tiene una propiedad dada. Por ejemplo, si P(x) es la propiedad "x es un número par", entonces ∃x P(x) es la proposición "Existe al menos un número par".

Conclusiones

El lenguaje formal es esencial para la lógica matemática, ya que permite expresar de manera precisa y rigurosa las ideas y conceptos. En este artículo, hemos visto las principales proposiciones, conectivas lógicas, variables y cuantificadores utilizados en la lógica matemática.

Si quieres profundizar en esta disciplina, te recomendamos estudiar con detenimiento estos conceptos y practicar su aplicación en ejercicios y problemas. De esta manera, podrás mejorar tu comprensión de la lógica matemática y comunicarte de manera efectiva en ella.

Preguntas frecuentes

¿Por qué es importante el lenguaje formal en la lógica matemática?

El lenguaje formal es importante en la lógica matemática porque permite expresar de manera precisa y rigurosa las ideas y conceptos. En esta disciplina, es esencial evitar la ambigüedad y la confusión en las proposiciones y argumentos, y el lenguaje formal es una herramienta valiosa para lograr este objetivo.

¿Qué son las proposiciones en la lógica matemática?

En la lógica matemática, una proposición es una afirmación que puede ser verdadera o falsa. Por ejemplo, "5 es un número par" es una proposición, que es verdadera, mientras que "2 + 2 = 5" es otra proposición, que es falsa.

¿Qué son las conectivas lógicas en la lógica matemática?

Las conectivas lógicas son símbolos que se utilizan para conectar proposiciones y formar nuevas proposiciones en la lógica matemática. Las principales conectivas lógicas son la negación, la conjunción, la disyunción, la implicación y la equivalencia.

¿Qué son las variables en la lógica matemática?

En la lógica matemática, las variables se utilizan para representar objetos o elementos de un conjunto. Por ejemplo, x puede representar un número real cualquiera.

¿Qué son los cuantificadores en la lógica matemática?

Los cuantificadores se utilizan para expresar la cantidad de elementos de un conjunto que satisfacen una propiedad dada en la lógica matemática. Los principales cuantificadores son el cuantificador universal (∀) y el cuantificador existencial (∃).