La lógica al descubierto: definición real y sencilla
La lógica es una disciplina que estudia el razonamiento humano, las formas de inferencia y la validez de los argumentos. Es una herramienta fundamental para la toma de decisiones y la resolución de problemas.
¿Qué es la lógica?
La lógica es una ciencia formal que se ocupa de estudiar las leyes y principios de la inferencia válida. Es decir, se encarga de analizar los argumentos para determinar si son verdaderos o falsos. La lógica no se ocupa del contenido de los argumentos, sino de su estructura.
¿Para qué sirve la lógica?
La lógica es una herramienta fundamental para la toma de decisiones y la resolución de problemas. Nos permite analizar la información de manera crítica y llegar a conclusiones razonadas. Además, la lógica es esencial en disciplinas como la filosofía, las matemáticas, la informática y la ciencia en general.
Principales ramas de la lógica
Existen varias ramas de la lógica, entre las más importantes se encuentran:
Lógica proposicional
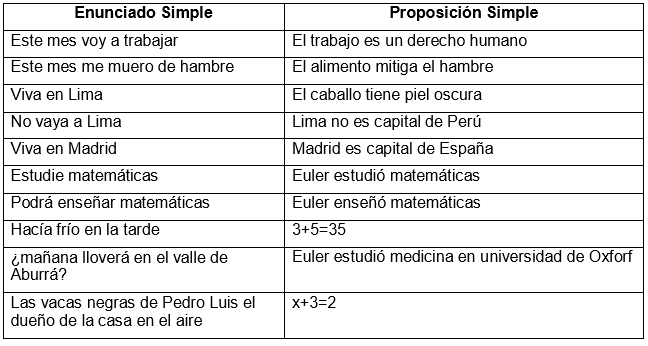
La lógica proposicional se ocupa del estudio de las proposiciones y su relación con los conectores lógicos (y, o, no, si...entonces). Esta rama de la lógica es muy útil para la simplificación de los argumentos y la identificación de falacias.
Lógica de predicados
La lógica de predicados se ocupa del estudio de las propiedades y relaciones entre los objetos. Esta rama de la lógica es fundamental en la matemática y la informática.
Lógica modal
La lógica modal se ocupa del estudio de los modos posibles de ser y de actuar. Esta rama de la lógica es muy útil en la filosofía y la teología.
Tipos de razonamiento
Existen varios tipos de razonamiento, entre los más importantes se encuentran:
Razonamiento deductivo
El razonamiento deductivo parte de una premisa o conjunto de premisas y llega a una conclusión necesariamente verdadera. Por ejemplo:
Premisa 1: Todos los hombres son mortales.
Premisa 2: Juan es un hombre.
Conclusión: Juan es mortal.
Razonamiento inductivo
El razonamiento inductivo parte de observaciones o casos particulares y llega a una conclusión probable. Por ejemplo:
Observación 1: Todos los cisnes que he visto son blancos.
Observación 2: Todos los cisnes que ha visto mi amigo son blancos.
Conclusión: Todos los cisnes son blancos.
Errores lógicos comunes
Existen varios errores lógicos comunes que debemos evitar, entre ellos:
Falacia ad hominem
Esta falacia consiste en atacar a la persona en lugar de sus argumentos. Por ejemplo, "No deberíamos seguir las políticas de Juan porque es un mentiroso".
Falacia de falsa dicotomía
Esta falacia consiste en presentar sólo dos opciones como si fueran las únicas posibles. Por ejemplo, "O estás con nosotros o estás contra nosotros".
Falacia de la pendiente resbaladiza
Esta falacia consiste en afirmar que una acción llevará a consecuencias negativas extremas, sin ofrecer pruebas. Por ejemplo, "Si aprobamos el matrimonio igualitario, pronto estaremos casándonos con animales".
Conclusión
La lógica es una herramienta fundamental para la toma de decisiones y la resolución de problemas. Nos permite analizar la información de manera crítica y llegar a conclusiones razonadas. Además, es esencial en disciplinas como la filosofía, las matemáticas, la informática y la ciencia en general.
Preguntas frecuentes
¿La lógica sólo se aplica en la filosofía?
No, la lógica se aplica en muchas disciplinas, como las matemáticas, la informática y la ciencia en general.
¿Qué es una falacia?
Una falacia es un error en el razonamiento que hace que un argumento sea inválido o poco convincente.
¿Cómo podemos evitar los errores lógicos?
Para evitar los errores lógicos, debemos aprender a reconocerlos y aplicar el pensamiento crítico en nuestra vida cotidiana.
¿La lógica es útil en la toma de decisiones cotidianas?
Sí, la lógica es una herramienta fundamental para la toma de decisiones cotidianas, ya que nos permite analizar la información de manera crítica y llegar a conclusiones razonadas.
¿Qué es el razonamiento inductivo?
El razonamiento inductivo parte de observaciones o casos particulares y llega a una conclusión probable.
Deja una respuesta