La importancia del álgebra booleana en la era digital

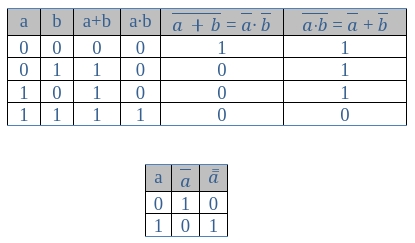
En la era digital en la que vivimos, donde la tecnología ha avanzado de manera exponencial, el álgebra booleana ha tomado una gran importancia en el mundo de la informática y la electrónica. Esta rama de la matemática se encarga del estudio de las proposiciones lógicas y sus operaciones, lo que ha permitido a los ingenieros y programadores desarrollar sistemas y dispositivos más complejos y eficientes.

¿Qué es el álgebra booleana?

El álgebra booleana es una rama de la matemática que se centra en el estudio de las proposiciones lógicas y sus operaciones. Esta rama se basa en la teoría de conjuntos y se utiliza en la electrónica y la informática para el diseño de circuitos lógicos y sistemas digitales.

El álgebra booleana se basa en dos valores: verdadero (representado por el número 1) y falso (representado por el número 0). A partir de estos valores, se pueden realizar diferentes operaciones lógicas, como la negación, la conjunción, la disyunción y la implicación.

¿Por qué es importante el álgebra booleana en la era digital?

El álgebra booleana es fundamental en la era digital ya que permite el diseño y desarrollo de sistemas y dispositivos más complejos y eficientes. La mayoría de los dispositivos electrónicos utilizados en la actualidad, como los ordenadores, los teléfonos móviles y los sistemas de control automático, están basados en circuitos lógicos que utilizan el álgebra booleana para su funcionamiento.

Además, el álgebra booleana es esencial para el desarrollo de algoritmos y programas informáticos. Los algoritmos son secuencias de instrucciones que permiten realizar operaciones complejas y el álgebra booleana es la base para el diseño de estas secuencias. Los programas informáticos, por su parte, están basados en el procesamiento de información lógica y el álgebra booleana es fundamental para su diseño y desarrollo.

Aplicaciones del álgebra booleana

El álgebra booleana tiene una amplia variedad de aplicaciones en la era digital. A continuación, se presentan algunas de las más relevantes:

Electrónica

En la electrónica, el álgebra booleana se utiliza en el diseño de circuitos lógicos y sistemas digitales. Los circuitos lógicos son sistemas electrónicos que realizan operaciones lógicas, como la negación, la conjunción y la disyunción, y están basados en el álgebra booleana.

Informática

En la informática, el álgebra booleana es fundamental en el diseño de algoritmos y programas informáticos. Los algoritmos son secuencias de instrucciones que permiten realizar operaciones complejas y el álgebra booleana es la base para el diseño de estas secuencias. Los programas informáticos, por su parte, están basados en el procesamiento de información lógica y el álgebra booleana es fundamental para su diseño y desarrollo.

Telecomunicaciones

En las telecomunicaciones, el álgebra booleana se utiliza en el diseño y desarrollo de sistemas de comunicaciones digitales. Estos sistemas se basan en la transmisión de señales digitales, que son procesadas mediante circuitos lógicos basados en el álgebra booleana.

Sistemas de control automático

En los sistemas de control automático, el álgebra booleana se utiliza en el diseño y desarrollo de sistemas de control digital. Estos sistemas se basan en la utilización de circuitos lógicos para el procesamiento de información y el álgebra booleana es fundamental para su diseño y desarrollo.

¿Cómo se aplica el álgebra booleana en la práctica?

En la práctica, el álgebra booleana se aplica mediante el diseño y desarrollo de circuitos lógicos y sistemas digitales. Estos circuitos y sistemas se basan en la utilización de operaciones lógicas, como la negación, la conjunción y la disyunción, para el procesamiento de información.

Para el diseño de estos circuitos y sistemas, se utilizan herramientas informáticas que permiten la simulación y verificación del funcionamiento de los mismos. Estas herramientas permiten la optimización de los circuitos y sistemas, lo que se traduce en una mayor eficiencia y menor consumo de energía.

Conclusión

El álgebra booleana es una rama de la matemática fundamental en la era digital. Su aplicación en la electrónica, la informática, las telecomunicaciones y los sistemas de control automático ha permitido el diseño y desarrollo de sistemas y dispositivos más complejos y eficientes. El álgebra booleana es esencial para el diseño de algoritmos y programas informáticos y se aplica mediante el diseño y desarrollo de circuitos lógicos y sistemas digitales.

Preguntas frecuentes

1. ¿Qué es el álgebra booleana?

El álgebra booleana es una rama de la matemática que se centra en el estudio de las proposiciones lógicas y sus operaciones.

2. ¿Por qué es importante el álgebra booleana en la era digital?

El álgebra booleana es importante en la era digital ya que permite el diseño y desarrollo de sistemas y dispositivos más complejos y eficientes.

3. ¿Cuáles son las aplicaciones del álgebra booleana?

El álgebra booleana tiene aplicaciones en la electrónica, la informática, las telecomunicaciones y los sistemas de control automático.

4. ¿Cómo se aplica el álgebra booleana en la práctica?

En la práctica, el álgebra booleana se aplica mediante el diseño y desarrollo de circuitos lógicos y sistemas digitales.

5. ¿Cómo se utiliza el álgebra booleana en el diseño de programas informáticos?

El álgebra booleana es fundamental en el diseño de algoritmos y programas informáticos, ya que es la base para el procesamiento de información lógica.