Funciones con lógica difusa: precisión en la toma de decisiones

La toma de decisiones es un proceso crucial en cualquier ámbito de la vida, desde el personal hasta el empresarial. Sin embargo, muchas veces la información que se tiene para tomar decisiones no es clara o precisa, lo que puede llevar a resultados subóptimos o incluso a errores. Es aquí donde la lógica difusa puede ser de gran utilidad.

¿Qué es la lógica difusa?

La lógica difusa es una rama de la inteligencia artificial que se encarga de tratar con información que es incierta, imprecisa o ambigua. En lugar de trabajar con valores binarios (verdadero o falso), la lógica difusa utiliza valores continuos entre 0 y 1 para representar la certeza o incertidumbre de una afirmación.

Por ejemplo, en lugar de decir que una persona es alta o baja, podemos usar la lógica difusa para decir que tiene una altura de 0.75 (en una escala de 0 a 1), lo que indica que su altura es más cercana a alta que a baja.

¿Cómo funciona la lógica difusa?

La lógica difusa utiliza conjuntos difusos, que son conjuntos de valores que no tienen una definición precisa. Por ejemplo, el conjunto difuso "personas altas" puede incluir personas que miden entre 1.70 y 1.90 metros, pero también puede incluir personas que miden un poco menos o un poco más si consideramos que la altura es un concepto relativo.

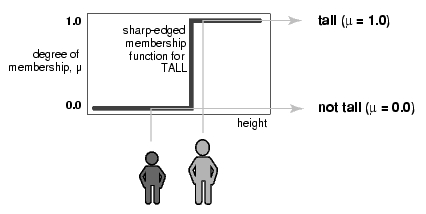
Para trabajar con conjuntos difusos, se utilizan funciones de membresía, que asignan un valor difuso a cada elemento del conjunto. Por ejemplo, podemos tener una función de membresía que asigna un valor de 0.2 a una persona que mide 1.60 metros y un valor de 0.8 a una persona que mide 1.80 metros.

Con estas funciones de membresía, podemos realizar operaciones lógicas difusas, como la unión, la intersección y la complementación de conjuntos difusos. De esta manera, podemos definir conceptos difusos como "personas altas y delgadas" o "días cálidos pero no demasiado calurosos".

Aplicaciones de la lógica difusa en la toma de decisiones

La lógica difusa tiene muchas aplicaciones en la toma de decisiones en diversos ámbitos. Algunas de las más comunes son:

Control de procesos

En el control de procesos, la lógica difusa se utiliza para ajustar los parámetros de un sistema en función de las condiciones cambiantes del entorno. Por ejemplo, en un sistema de climatización, podemos usar la lógica difusa para ajustar la temperatura y la humedad en función de la temperatura exterior y la cantidad de personas en la habitación.

Análisis de riesgos

En el análisis de riesgos, la lógica difusa se utiliza para evaluar la probabilidad de que ocurran ciertos eventos y sus posibles consecuencias. Por ejemplo, en la evaluación de riesgos de un proyecto de inversión, podemos usar la lógica difusa para evaluar la probabilidad de que el proyecto tenga éxito en función de diversos factores como la competencia, el mercado y la situación económica.

Diagnóstico médico

En el diagnóstico médico, la lógica difusa se utiliza para evaluar la probabilidad de que un paciente tenga cierta enfermedad en función de los síntomas y los resultados de los análisis clínicos. Por ejemplo, en el diagnóstico de enfermedades cardíacas, podemos usar la lógica difusa para evaluar la probabilidad de que un paciente tenga una enfermedad coronaria en función de factores como la edad, el sexo, la presión arterial y el colesterol.

Ventajas de la lógica difusa en la toma de decisiones

La lógica difusa tiene varias ventajas en comparación con otros enfoques de toma de decisiones. Algunas de las más importantes son:

Flexibilidad

La lógica difusa permite trabajar con información que es incierta o imprecisa, lo que la hace muy útil en situaciones en las que la información es limitada o difícil de interpretar.

Integración de conocimientos

La lógica difusa permite integrar conocimientos de diferentes fuentes y disciplinas, lo que puede llevar a decisiones más informadas y precisas.

Adaptación a cambios

La lógica difusa permite adaptarse a cambios en las condiciones del entorno, lo que la hace muy útil en situaciones dinámicas y cambiantes.

Conclusión

La lógica difusa es una herramienta poderosa para la toma de decisiones en situaciones en las que la información es incierta o imprecisa. Con su capacidad para trabajar con conjuntos difusos y funciones de membresía, la lógica difusa permite definir conceptos difusos y realizar operaciones lógicas difusas, lo que puede llevar a decisiones más informadas y precisas. Además, la lógica difusa tiene varias ventajas, como la flexibilidad, la integración de conocimientos y la adaptación a cambios.

Preguntas frecuentes

¿Qué es un conjunto difuso?

Un conjunto difuso es un conjunto de valores que no tienen una definición precisa. Por ejemplo, el conjunto difuso "personas altas" puede incluir personas que miden entre 1.70 y 1.90 metros, pero también puede incluir personas que miden un poco menos o un poco más si consideramos que la altura es un concepto relativo.

¿Qué es una función de membresía?

Una función de membresía es una función que asigna un valor difuso a cada elemento de un conjunto difuso. Por ejemplo, podemos tener una función de membresía que asigna un valor de 0.2 a una persona que mide 1.60 metros y un valor de 0.8 a una persona que mide 1.80 metros.

¿En qué ámbitos se utiliza la lógica difusa?

La lógica difusa se utiliza en diversos ámbitos, como el control de procesos, el análisis de riesgos, el diagnóstico médico y la toma de decisiones empresariales.

¿Cuáles son las ventajas de la lógica difusa en la toma de decisiones?

Entre las ventajas de la lógica difusa en la toma de decisiones se encuentran la flexibilidad, la integración de conocimientos y la adaptación a cambios.

¿Qué es una operación lógica difusa?

Una operación lógica difusa es una operación que se realiza sobre conjuntos difusos utilizando funciones de membresía. Algunas de las operaciones lógicas difusas más comunes son la unión, la intersección y la complementación de conjuntos difusos.