Fórmulas de Álgebra Booleana: ¡Simplifica tus operaciones!

El álgebra booleana es una rama de las matemáticas que se enfoca en el estudio de operaciones lógicas y sus propiedades. Esta disciplina juega un papel importante en el diseño de circuitos electrónicos, la programación de computadoras y en la lógica de proposiciones. En este artículo, exploraremos las fórmulas de álgebra booleana y cómo pueden simplificar tus operaciones.

¿Qué es el álgebra booleana?

El álgebra booleana se basa en dos valores lógicos: verdadero y falso (o 1 y 0, respectivamente). Estos valores se combinan mediante operaciones lógicas como la conjunción (AND), la disyunción (OR) y la negación (NOT). Por ejemplo, la expresión "A AND B" es verdadera solo si A y B son verdaderos, mientras que la expresión "A OR B" es verdadera si A o B (o ambos) son verdaderos.

¿Por qué simplificar las operaciones lógicas?

En muchos casos, las expresiones lógicas pueden ser muy complejas y difíciles de manejar. Simplificar estas expresiones puede ayudar a entenderlas mejor y a reducir el riesgo de errores en la implementación de circuitos o programas. Además, la simplificación puede reducir el tamaño y la complejidad de los circuitos o programas, lo que puede mejorar su eficiencia y reducir su costo.

Fórmulas de álgebra booleana para simplificar operaciones

Existen varias fórmulas de álgebra booleana que se pueden utilizar para simplificar operaciones lógicas. A continuación, se presentan algunas de las más comunes:

Identidades

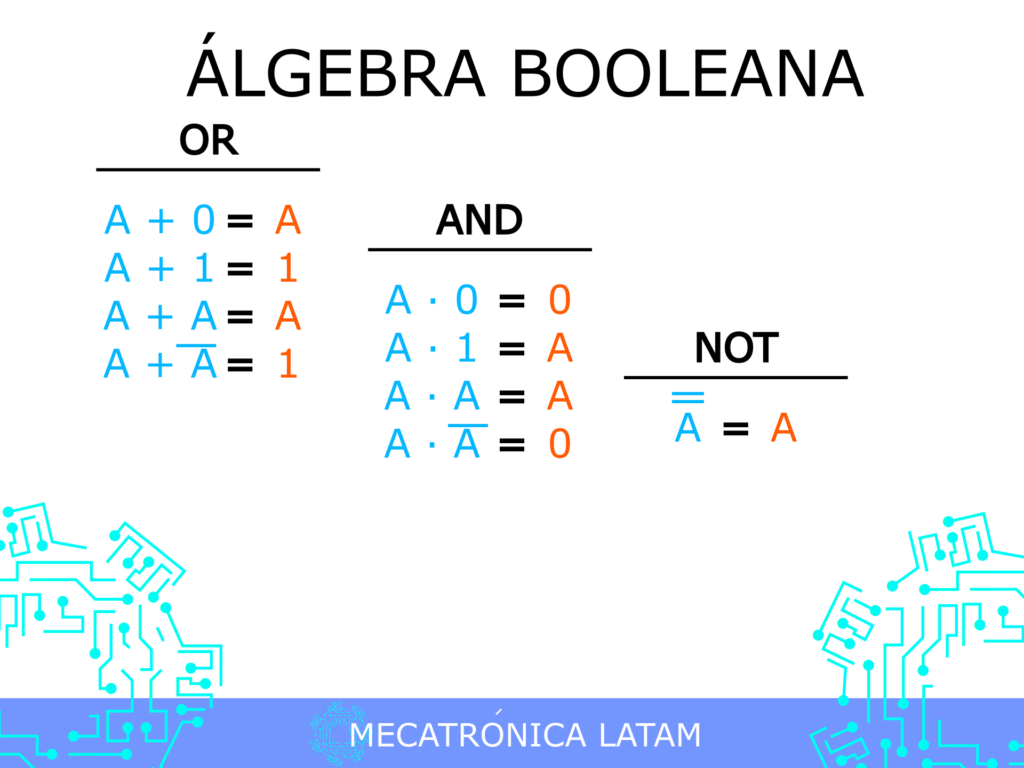
Las identidades son fórmulas que se aplican a una expresión y no cambian su valor. Algunas identidades comunes son:

• A AND 1 = A
• A OR 0 = A
• A OR 1 = 1
• A AND 0 = 0
• A AND A = A
• A OR A = A

Leyes de De Morgan

Las leyes de De Morgan son fórmulas que permiten transformar una expresión lógica en otra equivalente. Estas leyes son:

• NOT (A AND B) = NOT A OR NOT B
• NOT (A OR B) = NOT A AND NOT B

Teorema de la absorción

El teorema de la absorción dice que una expresión lógica puede ser simplificada eliminando los términos que se repiten en una operación AND y otra operación OR. Por ejemplo:

• A AND (A OR B) = A
• A OR (A AND B) = A

Teorema de la dualidad

El teorema de la dualidad establece que cualquier expresión lógica puede ser transformada en otra equivalente mediante el intercambio de las operaciones AND y OR, y la negación de todas las variables. Por ejemplo:

• NOT (A AND B) = NOT A OR NOT B
• NOT (A OR B) = NOT A AND NOT B
• A OR (B AND C) = (A OR B) AND (A OR C)
• A AND (B OR C) = (A AND B) OR (A AND C)

Aplicación de las fórmulas de álgebra booleana

Para aplicar las fórmulas de álgebra booleana, es necesario comprender las reglas básicas de las operaciones lógicas y tener habilidad para identificar patrones en las expresiones lógicas. A continuación, se presenta un ejemplo de cómo aplicar las fórmulas de álgebra booleana:

Supongamos que tenemos la expresión lógica A AND (B OR C) AND (B OR D). Podemos simplificar esta expresión utilizando el teorema de la absorción:

A AND (B OR C) AND (B OR D) = A AND (B OR C)

También podemos utilizar las leyes de De Morgan y las identidades para simplificar aún más esta expresión:

A AND (B OR C) = (A AND B) OR (A AND C)
(A AND B) OR (A AND C) = (A AND B) OR C

De esta manera, hemos simplificado la expresión original en (A AND B) OR C, que es una expresión mucho más simple y fácil de manejar.

Conclusión

El álgebra booleana es una disciplina importante en el diseño de circuitos electrónicos y la programación de computadoras. Las fórmulas de álgebra booleana permiten simplificar operaciones lógicas complejas y mejorar la eficiencia de los circuitos y programas. Al comprender y aplicar estas fórmulas, puedes simplificar tus operaciones lógicas y mejorar tu habilidad para implementar soluciones eficientes.

Preguntas frecuentes

1. ¿Qué es el álgebra booleana?

El álgebra booleana es una rama de las matemáticas que se enfoca en el estudio de operaciones lógicas y sus propiedades. Esta disciplina se basa en dos valores lógicos: verdadero y falso (o 1 y 0, respectivamente).

2. ¿Por qué es importante simplificar las operaciones lógicas?

Simplificar las operaciones lógicas puede ayudar a entenderlas mejor y a reducir el riesgo de errores en la implementación de circuitos o programas. Además, la simplificación puede reducir el tamaño y la complejidad de los circuitos o programas, lo que puede mejorar su eficiencia y reducir su costo.

3. ¿Cuáles son algunas fórmulas de álgebra booleana?

Algunas fórmulas de álgebra booleana comunes incluyen las identidades, las leyes de De Morgan, el teorema de la absorción y el teorema de la dualidad.

4. ¿Cómo se aplican las fórmulas de álgebra booleana?

Para aplicar las fórmulas de álgebra booleana, es necesario comprender las reglas básicas de las operaciones lógicas y tener habilidad para identificar patrones en las expresiones lógicas. Las fórmulas se utilizan para simplificar operaciones lógicas complejas y mejorar la eficiencia de los circuitos y programas.

5. ¿Cómo puedo mejorar mi habilidad en álgebra booleana?

Para mejorar tu habilidad en álgebra booleana, es recomendable estudiar las reglas básicas de las operaciones lógicas y practicar la simplificación de expresiones lógicas utilizando las fórmulas de álgebra booleana. También puedes utilizar herramientas de software especializado para facilitar la simplificación de operaciones lógicas complejas.