Fórmula para dividir un segmento en una razón dada: ¡Aprende ahora!

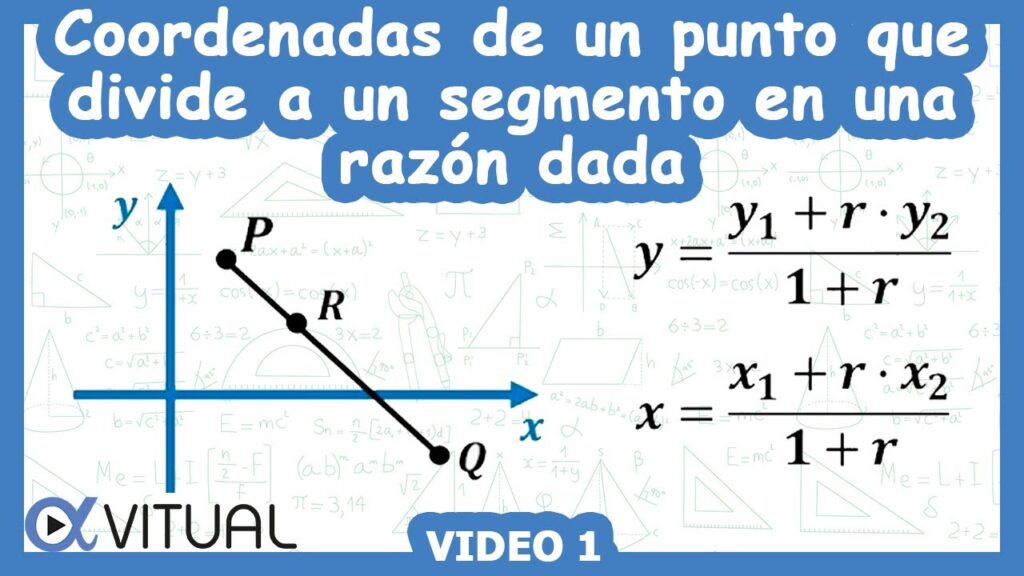
¿Alguna vez has tenido que dividir un segmento en una razón dada y no sabes cómo hacerlo? No te preocupes, en este artículo te enseñaremos una fórmula sencilla para lograrlo.

Antes de empezar, es importante tener en cuenta que esta fórmula se basa en la proporción. Es decir, si dos segmentos son proporcionales, entonces la razón entre ellos se mantiene constante. Por ejemplo, si el segmento AB es el doble de largo que el segmento CD, entonces la razón entre AB y CD siempre será de 2:1.

Ahora bien, para dividir un segmento en una razón dada, se deben seguir los siguientes pasos:

Paso 1: Identificar el segmento y la razón dada

Lo primero que debes hacer es identificar el segmento que deseas dividir y la razón en la que se debe dividir. Imagina que tienes el segmento AB y deseas dividirlo en la razón 2:1. En este caso, la razón indica que la parte más grande debe ser el doble de la parte más pequeña.

Paso 2: Dibujar una línea paralela al segmento

El siguiente paso es dibujar una línea paralela al segmento que deseas dividir. Esta línea debe estar ubicada en el extremo del segmento que corresponde a la parte más grande de la razón. En el ejemplo anterior, la línea debería estar ubicada en el extremo de AB que corresponde a la parte A.

Paso 3: Conectar los extremos del segmento con la línea paralela

Ahora, debes conectar los extremos del segmento con la línea paralela que acabas de dibujar. En el ejemplo, esto significa conectar los puntos A y B con la línea paralela que está ubicada en el extremo A de AB.

Paso 4: Identificar el punto de intersección

El siguiente paso es identificar el punto de intersección entre la línea paralela y la línea que conecta los extremos del segmento. Este punto se encuentra en el extremo del segmento que corresponde a la parte más pequeña de la razón. En el ejemplo, este punto se encuentra en la línea que conecta el punto B con la línea paralela.

Paso 5: Dividir el segmento en la razón dada

Una vez que has identificado el punto de intersección, puedes dividir el segmento en la razón dada. Para hacer esto, simplemente mide la distancia entre el punto de intersección y el extremo del segmento que corresponde a la parte más grande de la razón. Luego, mide la distancia entre el punto de intersección y el extremo del segmento que corresponde a la parte más pequeña de la razón. La primera distancia corresponde a la parte más grande de la razón, mientras que la segunda distancia corresponde a la parte más pequeña. En el ejemplo, si la distancia entre el punto de intersección y el punto A es de 6 cm, entonces la distancia entre el punto de intersección y el punto B debe ser de 3 cm.

Conclusión

Dividir un segmento en una razón dada puede ser una tarea sencilla si se sigue la fórmula adecuada. Es importante recordar que esta fórmula se basa en la proporción y que, por lo tanto, los segmentos deben ser proporcionales para que funcione. Si tienes dudas sobre cómo aplicar esta fórmula, no dudes en buscar ayuda de un profesor o tutor.

Preguntas frecuentes

1. ¿Es necesario que los segmentos sean proporcionales para aplicar la fórmula?

Sí, es necesario que los segmentos sean proporcionales para que la fórmula funcione.

2. ¿Puedo aplicar esta fórmula en cualquier tipo de segmento?

Sí, esta fórmula se puede aplicar en cualquier tipo de segmento siempre y cuando los segmentos sean proporcionales.

3. ¿Qué pasa si la razón dada no es un número entero?

Si la razón dada no es un número entero, se pueden utilizar fracciones o decimales para representarla.

4. ¿Por qué es importante dibujar una línea paralela al segmento?

Es importante dibujar una línea paralela al segmento para poder identificar el punto de intersección y dividir el segmento en la razón dada.

5. ¿Hay alguna otra forma de dividir un segmento en una razón dada?

Sí, existen otras formas de dividir un segmento en una razón dada, pero esta fórmula es una de las más sencillas y efectivas.