Fórmula lógica para tautología: ¡Verdadero siempre!

La lógica es una rama de la filosofía que se encarga del estudio de las formas del pensamiento y del razonamiento. Uno de los conceptos más importantes en lógica es el de tautología, que se refiere a una afirmación que es siempre verdadera, sin importar las circunstancias en las que se evalúe. En este artículo, hablaremos sobre la fórmula lógica para tautología y cómo se puede aplicar en diferentes contextos.

¿Qué es una tautología?

Antes de hablar sobre la fórmula lógica para tautología, es importante entender qué es una tautología. Una tautología es una afirmación que es siempre verdadera, sin importar las circunstancias en las que se evalúe. Por ejemplo, la afirmación "El sol es el sol" es una tautología, ya que es obvio que el sol es el sol, sin importar el momento o el lugar en el que se evalúe.

¿Cómo se puede identificar una tautología?

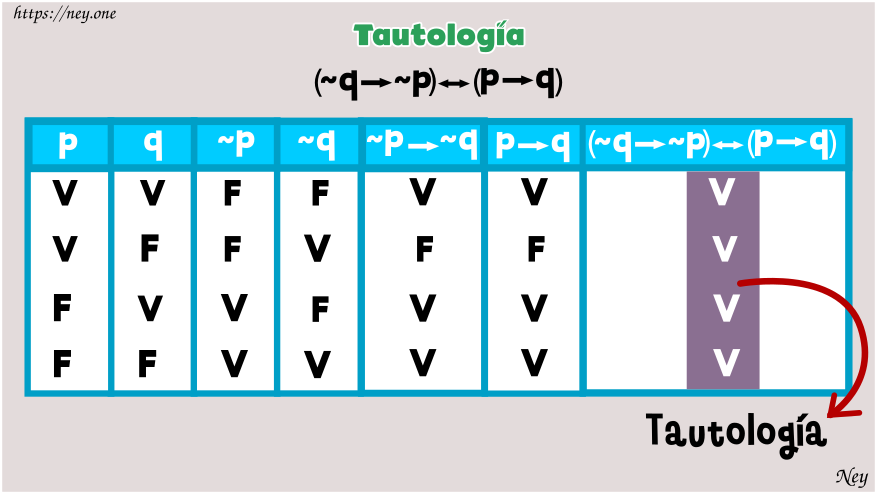
Hay varias maneras de identificar una tautología. Una forma común es utilizar tablas de verdad, que son herramientas lógicas que muestran todas las posibles combinaciones de valores de verdad para un conjunto de variables. Si todas las combinaciones posibles dan como resultado un valor verdadero, entonces la afirmación es una tautología.

Otra forma de identificar una tautología es mediante la aplicación de leyes lógicas, como la ley de identidad o la ley del tercio excluido. Si la afirmación cumple con estas leyes, entonces es una tautología.

La fórmula lógica para tautología

La fórmula lógica para tautología se basa en la idea de que una afirmación es una tautología si y solo si es posible demostrar que es verdadera utilizando solamente leyes lógicas. Esta fórmula se expresa de la siguiente manera:

A es una tautología si y solo si A es demostrable utilizando solamente leyes lógicas.

En otras palabras, si se puede demostrar que una afirmación es verdadera utilizando solamente leyes lógicas, entonces es una tautología.

Ejemplos de tautologías

Aquí hay algunos ejemplos de tautologías:

• El sol está arriba o no está arriba.
• La nieve es blanca o no es blanca.
• Un círculo es un círculo.

En cada uno de estos ejemplos, la afirmación es verdadera sin importar las circunstancias en las que se evalúe.

Aplicaciones de la fórmula lógica para tautología

La fórmula lógica para tautología tiene aplicaciones en diferentes contextos, incluyendo la informática, la matemática y la filosofía.

En informática, la fórmula lógica para tautología se utiliza para evaluar la validez de las expresiones booleanas en los programas de computadora. En matemáticas, se utiliza para demostrar la validez de los teoremas y las proposiciones. En filosofía, se utiliza para analizar argumentos y evaluar su validez.

Conclusión

La fórmula lógica para tautología es una herramienta importante en el estudio de la lógica. Nos permite identificar afirmaciones que son siempre verdaderas, sin importar las circunstancias en las que se evalúen. Esta fórmula tiene aplicaciones en diferentes contextos, incluyendo la informática, la matemática y la filosofía.

Preguntas frecuentes

1. ¿Qué es una tautología?

Una tautología es una afirmación que es siempre verdadera, sin importar las circunstancias en las que se evalúe.

2. ¿Cómo se puede identificar una tautología?

Se puede identificar una tautología utilizando tablas de verdad o aplicando leyes lógicas.

3. ¿Para qué se utiliza la fórmula lógica para tautología?

La fórmula lógica para tautología se utiliza para identificar afirmaciones que son siempre verdaderas y para evaluar la validez de expresiones, teoremas y argumentos.

4. ¿Qué aplicaciones tiene la fórmula lógica para tautología?

La fórmula lógica para tautología tiene aplicaciones en informática, matemáticas y filosofía.

5. ¿Cuál es la fórmula lógica para tautología?

La fórmula lógica para tautología se expresa de la siguiente manera: "A es una tautología si y solo si A es demostrable utilizando solamente leyes lógicas".