Formaliza la lógica proposicional: ¡Aprende cómo!
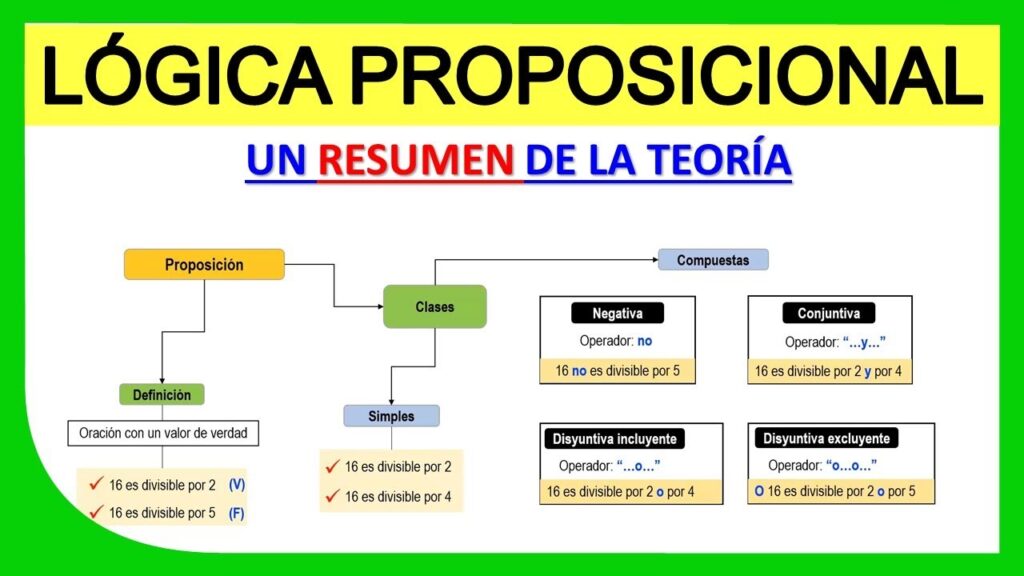
La lógica proposicional es una rama de la filosofía que se encarga del estudio de las proposiciones y sus relaciones lógicas. En otras palabras, la lógica proposicional se ocupa de analizar la forma en que las proposiciones se combinan para formar argumentos válidos. En este artículo, aprenderás cómo formalizar la lógica proposicional y crear argumentos sólidos.
¿Qué es la lógica proposicional?
La lógica proposicional es una rama de la lógica que se ocupa del estudio de las proposiciones y sus relaciones lógicas. Una proposición es una afirmación que puede ser verdadera o falsa. Por ejemplo, "el cielo es azul" es una proposición.
La lógica proposicional se encarga de analizar cómo las proposiciones se combinan para formar argumentos válidos. En la lógica proposicional, las proposiciones se representan mediante símbolos. Por ejemplo, "p" podría representar la proposición "el cielo es azul".
¿Por qué es importante formalizar la lógica proposicional?
Formalizar la lógica proposicional es importante porque permite analizar los argumentos de manera rigurosa y precisa. Cuando formalizamos la lógica proposicional, podemos representar las proposiciones mediante símbolos y analizarlas de manera más sistemática.
Además, la formalización de la lógica proposicional nos permite validar argumentos y demostrar si son válidos o no. Esto es especialmente útil en campos como las matemáticas, la informática y la filosofía, donde se utilizan argumentos lógicos de manera frecuente.
¿Cómo se formaliza la lógica proposicional?
Para formalizar la lógica proposicional, es necesario seguir algunos pasos básicos:
1. Identificar las proposiciones: Lo primero que debemos hacer es identificar las proposiciones que se están utilizando en el argumento. Por ejemplo, si el argumento es "Si llueve, entonces el suelo estará mojado", las proposiciones son "llueve" y "el suelo estará mojado".
2. Asignar símbolos a las proposiciones: Una vez que hemos identificado las proposiciones, debemos asignarles símbolos. Los símbolos más comunes en la lógica proposicional son las letras minúsculas del alfabeto, como "p", "q" y "r".
3. Identificar las conectivas lógicas: Las conectivas lógicas son los términos que se utilizan para unir proposiciones. Las más comunes son "y", "o" y "no". Por ejemplo, en el argumento "Si llueve y hace frío, entonces el suelo estará mojado", la conectiva lógica es "y".
4. Construir la expresión lógica: Una vez que hemos identificado las proposiciones y las conectivas lógicas, podemos construir la expresión lógica que representa el argumento. Por ejemplo, la expresión lógica para el argumento "Si llueve, entonces el suelo estará mojado" sería "p → q".
5. Analizar la expresión lógica: Una vez que hemos construido la expresión lógica, podemos analizarla para determinar si el argumento es válido o no. En la lógica proposicional, un argumento es válido si la conclusión se sigue necesariamente de las premisas.
Conclusión
La lógica proposicional es una herramienta fundamental para analizar argumentos y demostrar su validez. Al formalizar la lógica proposicional, podemos representar las proposiciones mediante símbolos y analizarlas de manera más sistemática. Si quieres mejorar tus habilidades lógicas y argumentativas, aprender a formalizar la lógica proposicional es un buen punto de partida.
Preguntas frecuentes
¿Qué es una proposición?
Una proposición es una afirmación que puede ser verdadera o falsa. Por ejemplo, "el cielo es azul" es una proposición.
¿Qué son las conectivas lógicas?
Las conectivas lógicas son los términos que se utilizan para unir proposiciones. Las más comunes son "y", "o" y "no".
¿Qué es una expresión lógica?
Una expresión lógica es una representación simbólica de una proposición o un argumento en la lógica proposicional.
¿Qué es un argumento válido?
En la lógica proposicional, un argumento es válido si la conclusión se sigue necesariamente de las premisas.
¿Para qué sirve la formalización de la lógica proposicional?
La formalización de la lógica proposicional sirve para analizar los argumentos de manera rigurosa y precisa, validar argumentos y demostrar si son válidos o no.
Deja una respuesta