Fe y razón: Matemáticos demuestran la existencia de Dios

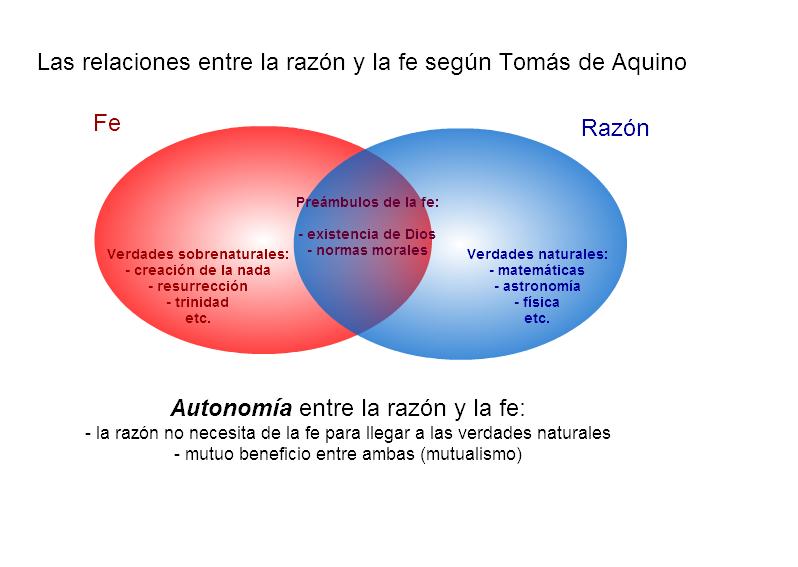
La relación entre la fe y la razón ha sido un tema de debate durante siglos. Mientras algunos argumentan que la fe es una cuestión de creencia sin necesidad de pruebas, otros defienden que la razón es esencial para entender la verdad sobre el mundo y Dios. En este contexto, algunos matemáticos han intentado demostrar la existencia de Dios usando herramientas matemáticas. ¿Es esto posible? En este artículo exploraremos el tema y presentaremos algunas de las pruebas matemáticas más famosas de la existencia de Dios.

¿Cómo se puede demostrar la existencia de Dios?

Antes de entrar en las pruebas matemáticas, es importante entender los diferentes enfoques que se han utilizado para demostrar la existencia de Dios. En general, se pueden distinguir dos tipos de pruebas: las pruebas a priori y las pruebas a posteriori.

Las pruebas a priori argumentan que la existencia de Dios puede ser demostrada a través de la razón y la lógica, sin necesidad de observar el mundo empírico. Estas pruebas se basan en la idea de que Dios es una necesidad lógica, como las verdades matemáticas.

Por otro lado, las pruebas a posteriori argumentan que la existencia de Dios puede ser demostrada a través de la observación del mundo empírico. Estas pruebas se basan en la idea de que el mundo y sus características apuntan hacia la existencia de un creador.

Las pruebas matemáticas de la existencia de Dios

A continuación, presentamos algunas de las pruebas matemáticas más famosas de la existencia de Dios.

1. La prueba ontológica de Anselmo de Canterbury

Esta prueba se basa en la idea de que Dios es el ser más perfecto que podemos imaginar. Anselmo argumenta que si Dios no existiera, no sería el ser más perfecto, ya que un ser perfecto tendría que existir en realidad. Por lo tanto, Dios existe necesariamente.

Esta prueba ha sido objeto de mucho debate y crítica, ya que se basa en la idea de que podemos definir la existencia de un ser simplemente a través de su definición. Sin embargo, muchos filósofos y matemáticos han intentado reformular la prueba para hacerla más sólida.

2. La prueba cosmológica de Gottfried Leibniz

Esta prueba se basa en la idea de que todo lo que existe tiene una causa. Si seguimos retrocediendo en el tiempo, llegaremos a una primera causa que no tuvo causa a su vez. Leibniz argumenta que esta primera causa es Dios.

Esta prueba también ha sido criticada por muchos, ya que se basa en la idea de que todo tiene una causa, lo cual no está necesariamente demostrado. Además, algunos argumentan que incluso si aceptamos que todo tiene una causa, no hay necesidad de que esa causa tenga que ser Dios.

3. La prueba del teorema de Gödel

Esta prueba se basa en un teorema matemático descubierto por Kurt Gödel en 1931. El teorema establece que en cualquier sistema formalizado lo suficientemente potente, siempre habrá verdades que no pueden ser demostradas dentro del sistema.

Algunos filósofos y matemáticos han argumentado que este teorema sugiere la existencia de verdades que están más allá de la capacidad humana para demostrar, y que estas verdades pueden incluir la existencia de Dios.

Sin embargo, esta interpretación del teorema ha sido criticada por otros, que argumentan que el teorema se aplica solo a sistemas formales y no tiene implicaciones para la existencia de Dios.

Conclusión

Aunque algunos matemáticos han intentado demostrar la existencia de Dios usando herramientas matemáticas, las pruebas han sido objeto de mucho debate y crítica. La relación entre la fe y la razón sigue siendo un tema complejo y difícil de resolver. Mientras algunos argumentan que la fe es una cuestión de creencia sin necesidad de pruebas, otros defienden que la razón es esencial para entender la verdad sobre el mundo y Dios.

Preguntas frecuentes

1. ¿Qué es la prueba ontológica de Anselmo?

La prueba ontológica de Anselmo argumenta que Dios existe necesariamente, ya que es el ser más perfecto que podemos imaginar. Esta prueba ha sido objeto de mucho debate y crítica, ya que se basa en la idea de que podemos definir la existencia de un ser simplemente a través de su definición.

2. ¿Qué es la prueba cosmológica de Leibniz?

La prueba cosmológica de Leibniz argumenta que todo lo que existe tiene una causa. Si seguimos retrocediendo en el tiempo, llegaremos a una primera causa que no tuvo causa a su vez. Leibniz argumenta que esta primera causa es Dios.

3. ¿Qué es el teorema de Gödel?

El teorema de Gödel es un teorema matemático que establece que en cualquier sistema formalizado lo suficientemente potente, siempre habrá verdades que no pueden ser demostradas dentro del sistema. Algunos filósofos y matemáticos han argumentado que este teorema sugiere la existencia de verdades que están más allá de la capacidad humana para demostrar, y que estas verdades pueden incluir la existencia de Dios.

4. ¿Por qué las pruebas matemáticas de la existencia de Dios han sido objeto de crítica?

Las pruebas matemáticas de la existencia de Dios han sido objeto de crítica porque se basan en supuestos que no están necesariamente demostrados, como la idea de que Dios es necesariamente el ser más perfecto que podemos imaginar, o la idea de que todo tiene una causa. Además, muchos argumentan que la existencia de Dios es una cuestión de fe, y que no puede ser demostrada a través de la razón.

5. ¿Qué relación hay entre la fe y la razón?

La relación entre la fe y la razón sigue siendo un tema complejo y difícil de resolver. Mientras algunos argumentan que la fe es una cuestión de creencia sin necesidad de pruebas, otros defienden que la razón es esencial para entender la verdad sobre el mundo y Dios. Sin embargo, muchos también argumentan que la fe y la razón pueden ser complementarias, y que ambas son necesarias para una comprensión completa de la realidad.