El infalible Teorema de Pitágoras: ¡siempre funciona!

El teorema de Pitágoras es una de las herramientas matemáticas más famosas y útiles de todos los tiempos. Este teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados. En otras palabras, a² + b² = c². Pero ¿por qué este teorema es tan importante y por qué siempre funciona?

Para entender por qué el teorema de Pitágoras siempre funciona, es importante comprender la geometría básica de un triángulo rectángulo. Un triángulo rectángulo tiene un ángulo recto (90 grados) y dos lados que forman ese ángulo recto. El lado opuesto al ángulo recto se llama hipotenusa y los otros dos lados se llaman catetos.

Cuando aplicamos el teorema de Pitágoras a un triángulo rectángulo, estamos buscando la relación entre los tres lados. El teorema dice que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Esto significa que podemos usar esta fórmula para encontrar la longitud de cualquier lado de un triángulo rectángulo si conocemos la longitud de los otros dos lados.

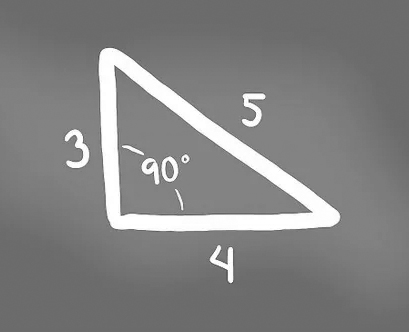
Por ejemplo, si sabemos que los catetos de un triángulo rectángulo miden 3 y 4 unidades, podemos encontrar la longitud de la hipotenusa usando el teorema de Pitágoras. La hipotenusa sería igual a la raíz cuadrada de 3² + 4², lo que da como resultado 5 unidades.

Pero, ¿por qué siempre funciona el teorema de Pitágoras? La respuesta es que se basa en la geometría básica de un triángulo rectángulo. Siempre que tengamos un triángulo rectángulo, podemos aplicar el teorema de Pitágoras para encontrar la relación entre los tres lados. No importa el tamaño del triángulo ni la ubicación de los ángulos, el teorema siempre funcionará.

Además, el teorema de Pitágoras tiene muchas aplicaciones prácticas en la vida cotidiana. Por ejemplo, los arquitectos lo usan para calcular la altura de un techo inclinado, los carpinteros lo usan para construir marcos de ventanas y los ingenieros lo usan para diseñar puentes y carreteras.

El teorema de Pitágoras es una herramienta matemática infalible que siempre funciona en cualquier triángulo rectángulo. Se basa en la geometría básica de un triángulo rectángulo y tiene muchas aplicaciones prácticas en la vida cotidiana. Siempre que necesites encontrar la relación entre los lados de un triángulo rectángulo, el teorema de Pitágoras es la herramienta perfecta.

Aplicaciones del Teorema de Pitágoras

El teorema de Pitágoras tiene muchas aplicaciones prácticas en la vida cotidiana, algunas de las cuales se enumeran a continuación:

Arquitectura

Los arquitectos lo usan para calcular la altura de un techo inclinado o la longitud de los lados de un edificio.

Carpintería

Los carpinteros lo usan para construir marcos de ventanas, escaleras y otras estructuras.

Ingeniería

Los ingenieros lo usan para diseñar puentes, carreteras y otros proyectos de construcción.

Navegación

Los navegantes lo usan para calcular la distancia entre dos puntos en un mapa.

Física

Los físicos lo usan para calcular la energía cinética de un objeto en movimiento.

Ejemplos prácticos del Teorema de Pitágoras

Para comprender mejor cómo funciona el teorema de Pitágoras, aquí hay algunos ejemplos prácticos:

Ejemplo 1

Supongamos que tenemos un triángulo rectángulo con catetos de 3 y 4 unidades. ¿Cuál es la longitud de la hipotenusa?

Usando el teorema de Pitágoras, podemos encontrar la longitud de la hipotenusa:

Hipotenusa² = Cateto1² + Cateto2²
Hipotenusa² = 3² + 4²
Hipotenusa² = 9 + 16
Hipotenusa² = 25
Hipotenusa = Raíz cuadrada de 25
Hipotenusa = 5 unidades

Por lo tanto, la longitud de la hipotenusa es 5 unidades.

Ejemplo 2

Supongamos que tenemos un triángulo rectángulo con una hipotenusa de 10 unidades y un cateto de 6 unidades. ¿Cuál es la longitud del otro cateto?

Usando el teorema de Pitágoras, podemos encontrar la longitud del otro cateto:

Hipotenusa² = Cateto1² + Cateto2²
10² = 6² + Cateto2²
100 = 36 + Cateto2²
Cateto2² = 64
Cateto2 = Raíz cuadrada de 64
Cateto2 = 8 unidades

Por lo tanto, la longitud del otro cateto es 8 unidades.

Conclusión

El teorema de Pitágoras es una herramienta matemática infalible que siempre funciona en cualquier triángulo rectángulo. Se basa en la geometría básica de un triángulo rectángulo y tiene muchas aplicaciones prácticas en la vida cotidiana. Siempre que necesites encontrar la relación entre los lados de un triángulo rectángulo, el teorema de Pitágoras es la herramienta perfecta.

Preguntas frecuentes

¿Qué es un triángulo rectángulo?

Un triángulo rectángulo es un triángulo que tiene un ángulo recto (90 grados) y dos lados que forman ese ángulo recto.

¿Qué es la hipotenusa?

La hipotenusa es el lado más largo de un triángulo rectángulo y se encuentra opuesta al ángulo recto.

¿Qué son los catetos?

Los catetos son los dos lados más cortos de un triángulo rectángulo que forman el ángulo recto.

¿Cómo se usa el teorema de Pitágoras?

El teorema de Pitágoras se usa para encontrar la relación entre los lados de un triángulo rectángulo. Se aplica la fórmula a² + b² = c², donde a y b son los catetos y c es la hipotenusa.

¿Cuáles son las aplicaciones del teorema de Pitágoras?

El teorema de Pitágoras tiene muchas aplicaciones prácticas en la vida cotidiana, incluyendo arquitectura, carpintería