El genio detrás de la teoría de conjuntos: Georg Cantor y su legado
La teoría de conjuntos es una rama fundamental de las matemáticas modernas. Su creador, Georg Cantor, fue un matemático alemán que vivió en el siglo XIX. Su trabajo en esta área revolucionó la forma en que los matemáticos piensan sobre el infinito y estableció las bases para muchos campos de investigación matemática, incluyendo la topología, la teoría de números y la lógica.
La vida de Georg Cantor
Georg Cantor nació en 1845 en la ciudad de San Petersburgo, Rusia, en una familia de origen alemán. Desde joven mostró una gran habilidad en matemáticas, pero también en música y literatura. Sin embargo, decidió dedicarse por completo a las matemáticas, estudiando en la Universidad de Berlín.
Después de graduarse, Cantor comenzó a trabajar en la teoría de los números, pero pronto se interesó en un problema que había fascinado a los matemáticos durante siglos: el infinito.
La teoría de conjuntos
El trabajo de Cantor en la teoría de conjuntos se inició en la década de 1870. La idea básica detrás de la teoría de conjuntos es que los objetos matemáticos pueden ser agrupados en conjuntos. Estos conjuntos pueden ser finitos o infinitos y pueden contener cualquier tipo de objeto matemático, desde números hasta funciones y más allá.
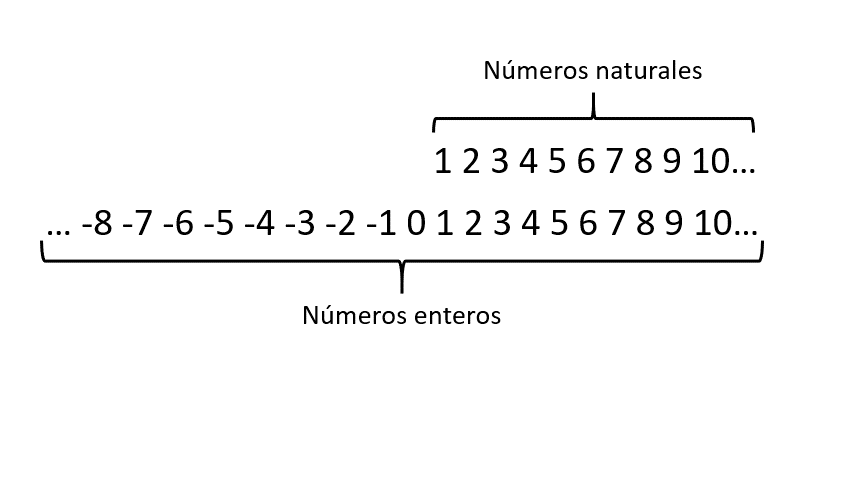
Cantor descubrió que hay diferentes tipos de infinitos. Por ejemplo, el conjunto de todos los números naturales es infinito, pero es diferente del conjunto de todos los números reales. Esta idea fue revolucionaria, ya que anteriormente se pensaba que todos los conjuntos infinitos eran iguales.
Cantor también propuso la idea de que hay diferentes tamaños de infinito. Por ejemplo, el conjunto de todos los números reales es más grande que el conjunto de todos los números naturales. Esta idea llevó a Cantor a desarrollar la teoría de los números transfinitos, que es una forma de medir el tamaño de los conjuntos infinitos.
El legado de Georg Cantor
El trabajo de Cantor en la teoría de conjuntos ha tenido un impacto duradero en las matemáticas y en otros campos. Su idea de que hay diferentes tipos y tamaños de infinitos ha llevado a nuevas formas de pensar sobre el infinito y ha inspirado a muchas áreas de investigación matemática.
Además, la teoría de conjuntos ha sido fundamental en la construcción de la lógica matemática moderna y ha influido en la filosofía y la física teórica.
Conclusión
Georg Cantor fue un genio matemático cuyo trabajo en la teoría de conjuntos ha tenido un impacto duradero en las matemáticas modernas y muchos otros campos. Su idea de que hay diferentes tipos y tamaños de infinitos ha llevado a nuevas formas de pensar sobre el infinito y ha inspirado a muchas áreas de investigación matemática.
Preguntas frecuentes
¿Cómo ha influido la teoría de conjuntos en las matemáticas modernas?
La teoría de conjuntos ha sido fundamental en la construcción de la lógica matemática moderna y ha influido en la filosofía y la física teórica. Además, ha llevado a nuevas formas de pensar sobre el infinito y ha inspirado a muchas áreas de investigación matemática.
¿Qué es la teoría de los números transfinitos?
La teoría de los números transfinitos es una forma de medir el tamaño de los conjuntos infinitos. Se utiliza para comparar diferentes tipos de infinitos y ha sido fundamental en la teoría de conjuntos.
¿Por qué la teoría de conjuntos ha sido tan influyente?
La teoría de conjuntos ha sido influyente porque ha llevado a nuevas formas de pensar sobre el infinito y ha inspirado a muchas áreas de investigación matemática. Además, ha sido fundamental en la construcción de la lógica matemática moderna y ha influido en la filosofía y la física teórica.
¿Qué otros campos han sido influenciados por la teoría de conjuntos?
La teoría de conjuntos ha influido en muchos campos, incluyendo la topología, la teoría de números y la lógica. También ha tenido un impacto en la filosofía y la física teórica.
¿Qué es un conjunto infinito?
Un conjunto infinito es un conjunto que tiene un número infinito de elementos. Puede ser un conjunto de números, funciones o cualquier otro tipo de objeto matemático.
Deja una respuesta