Ejercicios de lógica proposicional para secundaria

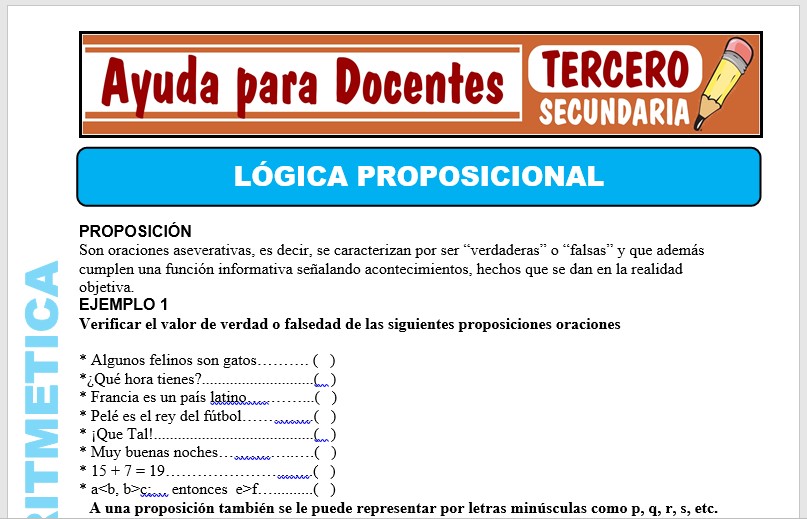
La lógica proposicional es una disciplina fundamental en el estudio de las matemáticas y la filosofía. Esta rama de la lógica se enfoca en el análisis y la evaluación de proposiciones, es decir, afirmaciones o enunciados que pueden ser verdaderos o falsos. En la educación secundaria, la lógica proposicional se introduce como una herramienta para desarrollar habilidades de pensamiento crítico y razonamiento deductivo. En este artículo, exploraremos algunos ejercicios de lógica proposicional para secundaria que pueden ayudar a los estudiantes a mejorar su capacidad de análisis y resolución de problemas.

1. Ejercicios de identificación de proposiciones

El primer paso en el estudio de la lógica proposicional es la identificación de proposiciones. Los estudiantes deben aprender a distinguir entre afirmaciones que pueden ser verdaderas o falsas y otras que no tienen sentido o no se pueden evaluar. Para estos ejercicios, los estudiantes pueden recibir una lista de enunciados y deben determinar cuáles de ellos son proposiciones y cuáles no.

Ejemplo:
- "La luna es un planeta" (proposición)
- "¡Qué bien suena esta canción!" (no es una proposición)
- "¿Cómo te llamas?" (no es una proposición)

2. Ejercicios de negación de proposiciones

La negación de una proposición es otra proposición que afirma lo contrario. Los estudiantes deben aprender a negar proposiciones correctamente. Para estos ejercicios, se puede presentar una proposición y pedir a los estudiantes que la nieguen.

Ejemplo:
Proposición: "El perro es negro"
Negación: "El perro no es negro"

3. Ejercicios de construcción de tablas de verdad

Las tablas de verdad son una herramienta que se utiliza para evaluar proposiciones complejas. Los estudiantes deben aprender a construir tablas de verdad y a utilizarlas para determinar la veracidad de una proposición. Para estos ejercicios, se puede presentar una proposición y pedir a los estudiantes que construyan su tabla de verdad correspondiente.

Ejemplo:
Proposición: "Si llueve, entonces me quedo en casa"
Tabla de verdad:
| Llueve | Me quedo en casa |
|--------|------------------|
| V | V |
| V | F |
| F | V |
| F | V |

4. Ejercicios de simplificación de proposiciones

Las proposiciones complejas pueden simplificarse utilizando las leyes de la lógica proposicional. Los estudiantes deben aprender a aplicar estas leyes para simplificar proposiciones y hacerlas más fáciles de entender. Para estos ejercicios, se puede presentar una proposición compleja y pedir a los estudiantes que la simplifiquen.

Ejemplo:
Proposición: "Si estudio, entonces sacaré buenas notas. Si saco buenas notas, entonces mis padres estarán contentos. Por lo tanto, si estudio, mis padres estarán contentos."
Simplificación: "Si estudio, mis padres estarán contentos."

5. Ejercicios de resolución de problemas

Finalmente, los estudiantes deben aprender a aplicar la lógica proposicional para resolver problemas prácticos. Se pueden presentar situaciones cotidianas y pedir a los estudiantes que utilicen la lógica proposicional para llegar a una conclusión lógica.

Ejemplo:
Sitación: "Si Ana no va al cine, entonces Juan no irá tampoco. Ana no va al cine. ¿Irán Juan y Pedro al cine?"
Solución: "Juan no irá al cine, pero no sabemos si Pedro irá o no."

Conclusión

La lógica proposicional es una habilidad fundamental que los estudiantes de secundaria deben aprender para desarrollar habilidades de pensamiento crítico y razonamiento deductivo. Los ejercicios de identificación de proposiciones, negación de proposiciones, construcción de tablas de verdad, simplificación de proposiciones y resolución de problemas son herramientas útiles para ayudar a los estudiantes a mejorar su capacidad de análisis y resolución de problemas.

Preguntas frecuentes

1. ¿Cómo puede la lógica proposicional ayudar a los estudiantes en su vida diaria?

La lógica proposicional puede ayudar a los estudiantes a tomar decisiones más informadas y a resolver problemas de manera más efectiva. Los estudiantes que comprenden la lógica proposicional pueden evaluar argumentos de manera más crítica y tomar decisiones fundamentadas en la evidencia.

2. ¿Hay alguna herramienta en línea que pueda ayudar a los estudiantes a practicar la lógica proposicional?

Sí, hay muchas herramientas en línea que pueden ayudar a los estudiantes a practicar la lógica proposicional. Algunos ejemplos incluyen Truth Table Generator, Logic Simulator y Logic Grid Puzzles.

3. ¿Por qué es importante aprender a simplificar proposiciones complejas?

Simplificar proposiciones complejas es importante porque ayuda a los estudiantes a comprender mejor la estructura lógica de una proposición. Al simplificar una proposición, los estudiantes pueden identificar las partes esenciales de la proposición y evaluar su veracidad de manera más efectiva.

4. ¿Cómo se puede incorporar la lógica proposicional en la enseñanza de otras materias?

La lógica proposicional puede ser útil en la enseñanza de muchas materias, incluyendo matemáticas, ciencias, filosofía y literatura. Los profesores pueden utilizar ejemplos de proposiciones en estas materias para enseñar a los estudiantes cómo analizar y evaluar proposiciones de manera efectiva.

5. ¿Cómo pueden los padres ayudar a sus hijos a practicar la lógica proposicional?

Los padres pueden ayudar a sus hijos a practicar la lógica proposicional al hacer preguntas lógicas y desafiantes en situaciones cotidianas. Por ejemplo, pueden preguntar a sus hijos cómo llegaron a una conclusión o pedirles que evalúen la veracidad de una afirmación. Los padres también pueden proporcionar a sus hijos recursos en línea para practicar la lógica proposicional.