Domina la lógica simbólica con ejercicios y tablas de verdad
La lógica simbólica es una rama de la filosofía que se encarga de estudiar el razonamiento a través de símbolos y fórmulas. En ella, los conceptos y proposiciones se representan de manera simbólica, lo que permite analizar y evaluar la validez de los argumentos de una forma más clara y precisa.
Si quieres aprender a dominar la lógica simbólica, es importante que conozcas algunos de sus conceptos básicos y que practiques con ejercicios y tablas de verdad. En este artículo, te explicaremos todo lo que necesitas saber para empezar.
Conceptos básicos de la lógica simbólica
Antes de empezar a resolver ejercicios y tablas de verdad, es importante que conozcas algunos de los conceptos básicos de la lógica simbólica:
Proposición
En lógica simbólica, una proposición es una afirmación que puede ser verdadera o falsa, pero no ambas al mismo tiempo. Por ejemplo, "el cielo es azul" es una proposición, mientras que "¿cómo estás?" no lo es, ya que no se puede determinar si es verdadera o falsa.
Conectivos lógicos
Los conectivos lógicos son símbolos que se utilizan para construir proposiciones más complejas a partir de proposiciones simples. Algunos de los más comunes son:
- Negación: se representa con el símbolo "~" y se utiliza para negar una proposición. Por ejemplo, "~p" significa "no p".
- Conjunción: se representa con el símbolo "^" y se utiliza para unir dos proposiciones con la condición de que ambas sean verdaderas. Por ejemplo, "p ^ q" significa "p y q".
- Disyunción: se representa con el símbolo "v" y se utiliza para unir dos proposiciones con la condición de que al menos una de ellas sea verdadera. Por ejemplo, "p v q" significa "p o q".
- Implicación: se representa con el símbolo "→" y se utiliza para indicar que la proposición de la izquierda implica la de la derecha. Por ejemplo, "p → q" significa "si p, entonces q".
- Equivalencia: se representa con el símbolo "↔" y se utiliza para indicar que dos proposiciones son equivalentes. Por ejemplo, "p ↔ q" significa "p si y solo si q".
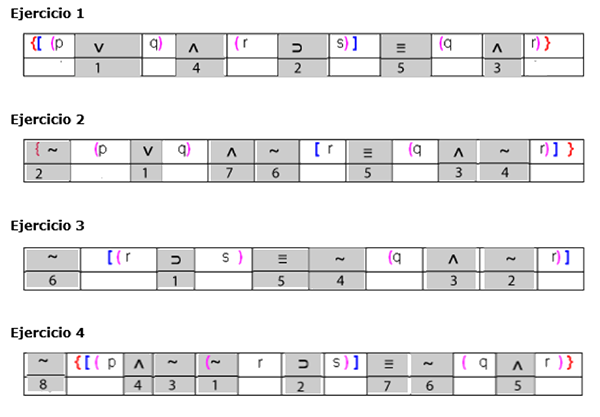
Ejercicios de lógica simbólica
Una de las mejores formas de aprender lógica simbólica es a través de la práctica. A continuación, te presentamos algunos ejercicios que puedes resolver para empezar:
Ejercicio 1
Identifica cuáles son las proposiciones simples y cuáles son las proposiciones compuestas en las siguientes proposiciones:
- "El cielo está nublado y está lloviendo"
- "Si estudias, aprobarás"
- "No es cierto que el sol salga por el oeste"
- "Juan es alto o Ana es baja"
Ejercicio 2
Construye la tabla de verdad para las siguientes proposiciones compuestas:
- "~p ^ q"
- "p v ~q"
- "p → q"
- "p ↔ q"
Tablas de verdad
Las tablas de verdad son una herramienta fundamental de la lógica simbólica, ya que permiten evaluar la validez de los argumentos y determinar si una proposición es verdadera o falsa en función de sus componentes. Para construir una tabla de verdad, se deben listar todas las posibles combinaciones de verdad o falsedad para cada proposición simple y, a partir de ellas, determinar el valor de verdad de la proposición compuesta.
A continuación, te mostramos un ejemplo de cómo construir una tabla de verdad para la proposición "p ^ q":
| p | q | p ^ q |
|---|---|-------|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
En este caso, se listan todas las posibles combinaciones de verdad o falsedad para las proposiciones p y q, y se determina el valor de verdad de p ^ q en función de ellas. Como se puede observar, la proposición es verdadera solo cuando ambas proposiciones simples son verdaderas.
Conclusión
La lógica simbólica es una herramienta útil para analizar y evaluar la validez de los argumentos. Para dominarla, es importante conocer los conceptos básicos y practicar con ejercicios y tablas de verdad. Si te interesa profundizar en este tema, te recomendamos que consultes más recursos y que sigas practicando.
Preguntas frecuentes
1. ¿Qué es una proposición en lógica simbólica?
Una proposición es una afirmación que puede ser verdadera o falsa, pero no ambas al mismo tiempo.
2. ¿Qué son los conectivos lógicos?
Los conectivos lógicos son símbolos que se utilizan para construir proposiciones más complejas a partir de proposiciones simples.
3. ¿Cómo se construye una tabla de verdad?
Para construir una tabla de verdad, se deben listar todas las posibles combinaciones de verdad o falsedad para cada proposición simple y, a partir de ellas, determinar el valor de verdad de la proposición compuesta.
4. ¿Por qué son útiles las tablas de verdad?
Las tablas de verdad son útiles porque permiten evaluar la validez de los argumentos y determinar si una proposición es verdadera o falsa en función de sus componentes.
5. ¿Cómo puedo practicar más con lógica simbólica?
Puedes practicar más con lógica simbólica resolviendo ejercicios y consultando recursos en línea. También puedes buscar cursos o tutoriales que te enseñen más sobre este tema.
Deja una respuesta