Domina la lógica proposicional y aplica la ley de Morgan

La lógica proposicional es una herramienta fundamental en el campo de las matemáticas y la informática. Se utiliza para analizar y evaluar la verdad o falsedad de las proposiciones, lo que es esencial para la toma de decisiones y la resolución de problemas. Una de las leyes más importantes en la lógica proposicional es la ley de Morgan, que permite simplificar la lógica y hacer más eficiente el razonamiento. En este artículo, aprenderás todo lo que necesitas saber para dominar la lógica proposicional y aplicar la ley de Morgan.

¿Qué es la lógica proposicional?

La lógica proposicional es un sistema formal que se utiliza para analizar y evaluar la verdad o falsedad de las proposiciones. Las proposiciones son declaraciones que pueden ser verdaderas o falsas, y se representan mediante variables proposicionales. Estas variables se pueden combinar utilizando conectivas lógicas, como la conjunción, la disyunción y la negación, para crear proposiciones más complejas.

Por ejemplo, si A es una proposición que significa "hace sol", y B es una proposición que significa "voy a la playa", podemos combinarlas utilizando la conjunción (representada por el símbolo ∧) para crear la proposición "hace sol ∧ voy a la playa". Esta proposición es verdadera solo si ambas proposiciones individuales son verdaderas.

¿Qué es la ley de Morgan?

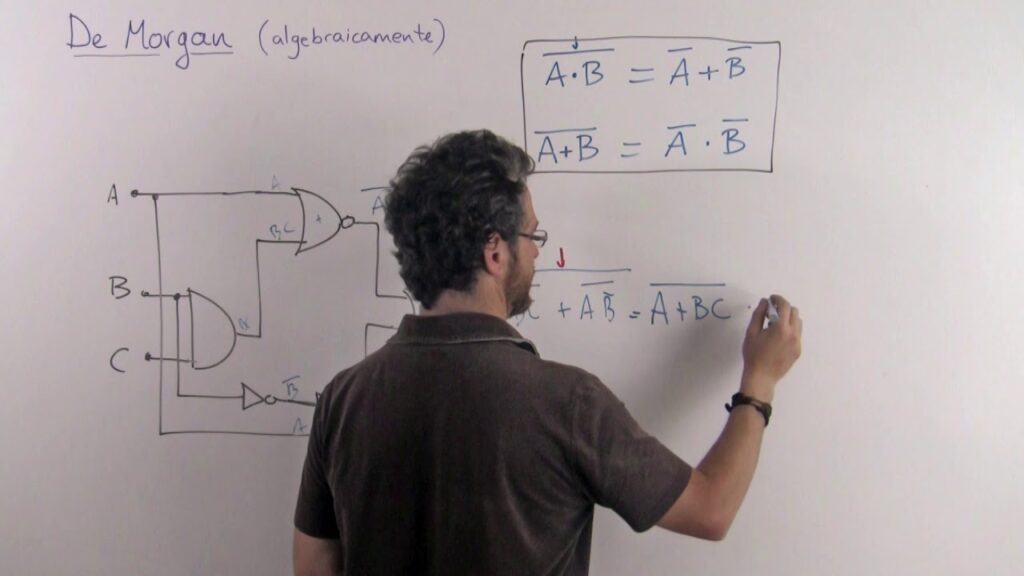
La ley de Morgan es una regla fundamental en la lógica proposicional que permite simplificar la lógica y hacer más eficiente el razonamiento. Esta ley establece que la negación de una conjunción (A ∧ B) es equivalente a la disyunción de las negaciones de las proposiciones individuales (¬A ∨ ¬B), y que la negación de una disyunción (A ∨ B) es equivalente a la conjunción de las negaciones de las proposiciones individuales (¬A ∧ ¬B).

En otras palabras, si queremos negar una proposición que es una conjunción o una disyunción, podemos aplicar la ley de Morgan para crear una proposición equivalente que sea más fácil de analizar y evaluar.

Cómo aplicar la ley de Morgan

Para aplicar la ley de Morgan, sigue estos sencillos pasos:

1. Identifica la proposición que quieres negar.

2. Si la proposición es una conjunción (A ∧ B), cambia el operador ∧ por ∨ y niega cada proposición individual para obtener ¬A ∨ ¬B.

3. Si la proposición es una disyunción (A ∨ B), cambia el operador ∨ por ∧ y niega cada proposición individual para obtener ¬A ∧ ¬B.

4. Evalúa la proposición resultante para determinar su verdad o falsedad.

Por ejemplo, si queremos negar la proposición "hace sol y hace calor", podemos aplicar la ley de Morgan para obtener la proposición equivalente "no hace sol o no hace calor". Esta proposición es verdadera si al menos una de las proposiciones individuales es falsa.

Ejemplos de aplicación de la ley de Morgan

Veamos algunos ejemplos de cómo aplicar la ley de Morgan en la práctica:

1. Negar la proposición "es lunes y tengo que trabajar":
- Cambiamos el operador ∧ por ∨ y negamos cada proposición individual para obtener "no es lunes o no tengo que trabajar".

2. Negar la proposición "estudio matemáticas o física":
- Cambiamos el operador ∨ por ∧ y negamos cada proposición individual para obtener "no estudio matemáticas y no estudio física".

3. Negar la proposición "tengo más de 18 años y soy menor de edad":
- Cambiamos el operador ∧ por ∨ y negamos cada proposición individual para obtener "tengo menos de 18 años o no soy menor de edad".

Conclusión

La lógica proposicional y la ley de Morgan son herramientas fundamentales para el análisis y la evaluación de proposiciones. Al dominar la lógica proposicional y aplicar la ley de Morgan, podrás simplificar la lógica y hacer más eficiente el razonamiento. Esperamos que este artículo te haya sido útil para comprender estos conceptos y aplicarlos en la práctica.

Preguntas frecuentes

1. ¿Qué es una proposición en la lógica proposicional?
- Una proposición es una declaración que puede ser verdadera o falsa, y se representa mediante variables proposicionales.

2. ¿Qué son las conectivas lógicas en la lógica proposicional?
- Las conectivas lógicas son operadores que se utilizan para combinar proposiciones y crear proposiciones más complejas. Algunas de las conectivas lógicas son la conjunción, la disyunción y la negación.

3. ¿Por qué es importante aplicar la ley de Morgan en la lógica proposicional?
- La ley de Morgan permite simplificar la lógica y hacer más eficiente el razonamiento al crear proposiciones equivalentes que son más fáciles de analizar y evaluar.

4. ¿Cómo puedo saber si una proposición es verdadera o falsa en la lógica proposicional?
- Puedes evaluar una proposición en función del valor de verdad de las proposiciones individuales y las conectivas lógicas que se utilizan para combinarlas.

5. ¿Dónde se utiliza la lógica proposicional en la vida diaria?
- La lógica proposicional se utiliza en campos como las matemáticas, la informática, la filosofía y la ciencia para analizar y evaluar proposiciones y resolver problemas.