Domina el sistema numérico con álgebra booleana
Si alguna vez has trabajado con electrónica digital, programación de computadoras, redes de computadoras o cualquier otro campo relacionado con la tecnología de la información, es probable que hayas oído hablar del álgebra booleana. Esta rama de la matemática se centra en el estudio de los sistemas numéricos que solo tienen dos valores posibles, generalmente representados como 0 y 1. Los matemáticos a menudo se refieren a estos valores como "falso" y "verdadero", respectivamente, y utilizan una variedad de operadores lógicos para manipularlos y crear circuitos digitales complejos.
En este artículo, te llevaremos a través de los conceptos fundamentales del álgebra booleana, incluyendo los diferentes operadores lógicos que se utilizan, así como algunas aplicaciones prácticas de esta rama de las matemáticas.
¿Qué es el álgebra booleana?
El álgebra booleana es una rama de la matemática que se centra en el estudio de sistemas numéricos que solo tienen dos valores posibles: 0 y 1 (o falso y verdadero). Esta rama de la matemática fue desarrollada por el matemático británico George Boole en la década de 1850, y desde entonces ha sido ampliamente utilizada en una variedad de campos de la tecnología de la información.
Operadores lógicos
Para manipular los valores en un sistema numérico booleano, se utilizan una variedad de operadores lógicos. Estos operadores se utilizan para realizar diferentes operaciones en los valores booleanos, como negarlos, compararlos y combinarlos.
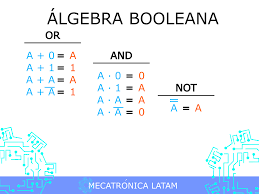
Operador NOT
El operador NOT se utiliza para negar un valor booleano. Si el valor original es verdadero, el operador NOT lo convierte en falso, y viceversa. En términos matemáticos, el operador NOT se representa con una barra encima de un valor booleano. Por ejemplo, si tenemos un valor booleano A que es verdadero, la expresión NOT A se escribiría como ¬A y sería falsa.
Operador AND
El operador AND se utiliza para comparar dos valores booleanos. Si ambos valores son verdaderos, el resultado es verdadero. Si uno o ambos valores son falsos, el resultado es falso. En términos matemáticos, el operador AND se representa con el símbolo "&". Por ejemplo, si tenemos dos valores booleanos A y B que son verdaderos, la expresión A & B sería verdadera.
Operador OR
El operador OR se utiliza para combinar dos valores booleanos. Si uno o ambos valores son verdaderos, el resultado es verdadero. Si ambos valores son falsos, el resultado es falso. En términos matemáticos, el operador OR se representa con el símbolo "|". Por ejemplo, si tenemos dos valores booleanos A y B, donde A es verdadero y B es falso, la expresión A | B sería verdadera.
Operador XOR
El operador XOR se utiliza para comparar dos valores booleanos y producir un resultado verdadero si los valores son diferentes. Si los valores son iguales, el resultado es falso. En términos matemáticos, el operador XOR se representa con el símbolo "^". Por ejemplo, si tenemos dos valores booleanos A y B, donde A es verdadero y B es falso, la expresión A ^ B sería verdadera.
Aplicaciones prácticas del álgebra booleana
El álgebra booleana tiene una variedad de aplicaciones prácticas en la tecnología de la información. Algunas de estas aplicaciones incluyen:
Circuitos digitales
El álgebra booleana se utiliza para diseñar y analizar circuitos digitales. Los circuitos digitales son componentes electrónicos que solo pueden estar en uno de dos estados posibles: encendido o apagado. El álgebra booleana se utiliza para diseñar circuitos digitales que realizan operaciones lógicas complejas, como la adición y la multiplicación.
Programación de computadoras
El álgebra booleana se utiliza en la programación de computadoras para crear expresiones lógicas que determinan el flujo del programa. Las expresiones lógicas se utilizan para controlar las condiciones en las que se ejecutan diferentes partes del programa.
Redes de computadoras
El álgebra booleana se utiliza en las redes de computadoras para establecer reglas de enrutamiento y filtrado de paquetes. Las reglas se basan en expresiones lógicas que determinan si un paquete debe ser permitido o denegado en función de su dirección de origen, dirección de destino y otros factores.
Conclusión
El álgebra booleana es una rama fascinante de la matemática que se centra en el estudio de sistemas numéricos que solo tienen dos valores posibles: 0 y 1. Esta rama de la matemática es ampliamente utilizada en la tecnología de la información para diseñar circuitos digitales, programar computadoras y establecer reglas de enrutamiento y filtrado de paquetes en las redes de computadoras. Si estás interesado en la tecnología de la información, dominar el álgebra booleana es una habilidad esencial que te permitirá trabajar con sistemas digitales complejos.
Preguntas frecuentes
1. ¿Qué es un sistema numérico booleano?
Un sistema numérico booleano es un sistema numérico que solo tiene dos valores posibles: 0 y 1. Estos valores se utilizan para representar los conceptos de falso y verdadero, respectivamente.
2. ¿Qué operadores lógicos se utilizan en el álgebra booleana?
Los operadores lógicos utilizados en el álgebra booleana incluyen NOT, AND, OR y XOR. Estos operadores se utilizan para manipular los valores booleanos y realizar operaciones lógicas complejas.
3. ¿Para qué se utiliza el álgebra booleana en la programación de computadoras?
El álgebra booleana se utiliza en la programación de computadoras para crear expresiones lógicas que determinan el flujo del programa. Las expresiones lógicas se utilizan para controlar las condiciones en las que se ejecutan diferentes partes del programa.
4. ¿Qué son los circuitos digitales?
Los circuitos digitales son componentes electrónicos que solo pueden estar en uno de dos estados posibles: encendido o apagado. El álgebra booleana se utiliza para diseñar circuitos digitales que realizan operaciones lógicas complejas, como la adición y la multiplicación.
5. ¿Cómo se utiliza el álgebra booleana en las redes de computadoras?
El álgebra booleana se utiliza en las redes de computadoras para establecer reglas de enrutamiento y filtrado de paquetes. Las reglas se basan en expresiones lógicas que determinan si un paquete debe ser permitido o denegado en función de su dirección de origen, dirección de destino y otros factores.
Deja una respuesta