Domina el álgebra booleana con el método Karnaugh
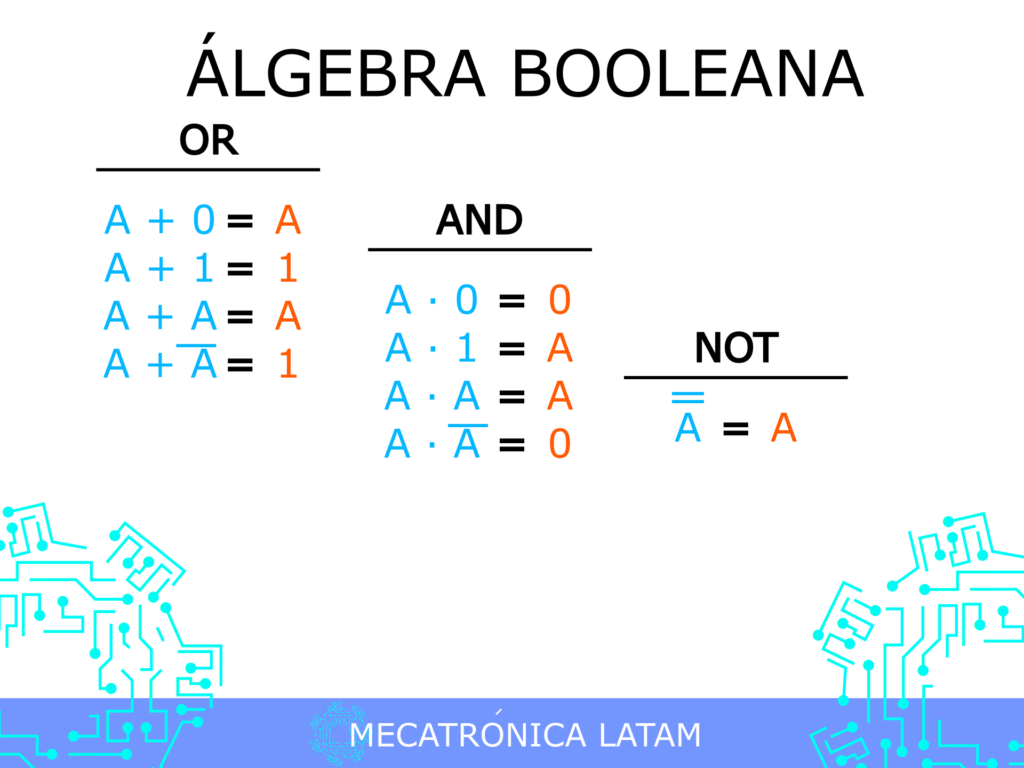
El álgebra booleana es una rama de las matemáticas que se dedica al estudio de las operaciones lógicas y las variables binarias. Esta disciplina es fundamental en el diseño de circuitos digitales, sistemas de control y programación de computadoras. Una de las herramientas más útiles para simplificar expresiones booleanas es el método Karnaugh, que permite reducir complejas ecuaciones lógicas de manera intuitiva y sencilla. En este artículo, te explicaremos cómo funciona este método y cómo puedes aplicarlo para resolver problemas de álgebra booleana.
¿Qué es el álgebra booleana?
El álgebra booleana es un campo de las matemáticas que se enfoca en el estudio de las operaciones lógicas y las variables binarias. La lógica booleana se basa en dos valores, verdadero (1) y falso (0), que se combinan mediante operadores lógicos como AND, OR y NOT. Estas operaciones se utilizan para construir expresiones lógicas que describen el comportamiento de sistemas digitales y de computadoras.
¿Qué es el método Karnaugh?
El método Karnaugh, también conocido como mapa de Karnaugh o tabla de Karnaugh, es una técnica para simplificar expresiones booleanas. Fue desarrollado por el matemático indio Maurice Karnaugh en la década de 1950 y se basa en la representación visual de las variables booleanas en una tabla de dos dimensiones.
¿Cómo funciona el método Karnaugh?
El método Karnaugh se basa en la agrupación de términos en la tabla de Karnaugh. Para ello, se representan las variables booleanas en una tabla de dos dimensiones, donde cada combinación de valores se representa mediante un cuadro. Para una variable booleana, la tabla tiene dos filas y dos columnas. Para dos variables, la tabla tiene cuatro filas y cuatro columnas, y así sucesivamente.
Una vez que se ha representado la expresión booleana en la tabla de Karnaugh, se procede a agrupar los términos que tienen valores verdaderos (1) en grupos de dos, cuatro, ocho, etc. Estos grupos se deben formar de forma contigua, es decir, sin saltar filas o columnas en la tabla. Cada grupo se representa mediante una letra, que corresponde a los valores de las variables que se encuentran en el grupo. Por ejemplo, si se agrupan los términos que tienen las variables A y B verdaderas, se obtiene el grupo AB.
Una vez que se han agrupado todos los términos posibles, se procede a simplificar la expresión booleana mediante la eliminación de los términos redundantes. Para ello, se buscan grupos que se solapen y se eliminan los términos que se repiten. La expresión booleana simplificada se obtiene al unir los términos que quedan después de la eliminación de los términos redundantes.
¿Cómo se aplica el método Karnaugh?
El método Karnaugh se puede aplicar para simplificar cualquier expresión booleana, por compleja que sea. Para ello, se deben seguir los siguientes pasos:
1. Representar la expresión booleana en la tabla de Karnaugh.
2. Agrupar los términos que tienen valores verdaderos (1) en grupos de dos, cuatro, ocho, etc.
3. Simplificar la expresión booleana eliminando los términos redundantes.
4. Escribir la expresión booleana simplificada.
¿Cuáles son las ventajas del método Karnaugh?
El método Karnaugh tiene varias ventajas sobre otros métodos de simplificación de expresiones booleanas. En primer lugar, es fácil de aprender y aplicar, ya que se basa en la representación visual de las variables booleanas en una tabla de dos dimensiones. En segundo lugar, es intuitivo y permite la simplificación de ecuaciones complejas de manera rápida y sencilla. Finalmente, es una herramienta útil para el diseño de circuitos digitales y sistemas de control, ya que permite la reducción del número de puertas lógicas y la simplificación de las ecuaciones que describen su funcionamiento.
Conclusión
El método Karnaugh es una herramienta poderosa para simplificar expresiones booleanas en el álgebra booleana. Permite la reducción de ecuaciones complejas de manera intuitiva y sencilla, lo que lo convierte en una herramienta esencial para el diseño de circuitos digitales y sistemas de control. Si quieres dominar el álgebra booleana, el método Karnaugh es una técnica que debes aprender.
Preguntas frecuentes
¿Qué es el álgebra booleana?
El álgebra booleana es un campo de las matemáticas que se enfoca en el estudio de las operaciones lógicas y las variables binarias. La lógica booleana se basa en dos valores, verdadero (1) y falso (0), que se combinan mediante operadores lógicos como AND, OR y NOT.
¿Para qué se utiliza el álgebra booleana?
El álgebra booleana se utiliza en el diseño de circuitos digitales, sistemas de control y programación de computadoras. Es una herramienta fundamental para describir el comportamiento de sistemas digitales y para simplificar ecuaciones lógicas complejas.
¿Qué es el método Karnaugh?
El método Karnaugh es una técnica para simplificar expresiones booleanas. Fue desarrollado por el matemático indio Maurice Karnaugh en la década de 1950 y se basa en la representación visual de las variables booleanas en una tabla de dos dimensiones.
¿Cómo se aplica el método Karnaugh?
El método Karnaugh se aplica mediante la representación de la expresión booleana en la tabla de Karnaugh, la agrupación de los términos que tienen valores verdaderos (1), la simplificación de la expresión eliminando los términos redundantes, y la escritura de la expresión booleana simplificada.
¿Cuáles son las ventajas del método Karnaugh?
Las ventajas del método Karnaugh son su facilidad de aprendizaje y aplicación, su intuición para simplificar ecuaciones complejas, y su utilidad para el diseño de circuitos digitales y sistemas de control.
Deja una respuesta