Determinando axiomas: la base de la lógica y la matemática

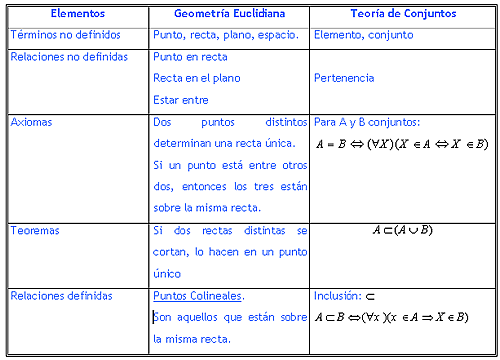
La lógica y la matemática son dos disciplinas que tienen una base común: los axiomas. Los axiomas son enunciados que se consideran verdaderos sin necesidad de demostración previa, y a partir de ellos se desarrollan los teoremas y las demostraciones que permiten construir sistemas lógicos y matemáticos sólidos.

Pero, ¿cómo se determinan los axiomas? ¿Son universales o dependen del contexto en el que se aplican? En este artículo, exploraremos el papel de los axiomas en la lógica y la matemática, y veremos cómo se establecen y utilizan en cada disciplina.

¿Qué son los axiomas?

Los axiomas son enunciados que se consideran verdaderos por sí mismos, sin necesidad de demostración previa. Son la base de cualquier sistema lógico o matemático, ya que a partir de ellos se derivan los teoremas y las demostraciones que permiten establecer la validez de las proposiciones y los argumentos.

Por ejemplo, en la geometría euclidiana, uno de los axiomas es que por un punto exterior a una recta puede trazarse una única recta paralela a la recta dada. Este axioma es fundamental para la construcción de todo el sistema geométrico, ya que a partir de él se pueden demostrar otros teoremas y proposiciones.

Cómo se determinan los axiomas

La determinación de los axiomas es un proceso complejo que depende en gran medida del contexto en el que se aplican. En algunos casos, los axiomas son universales y se consideran verdaderos en cualquier situación. En otros casos, los axiomas dependen del sistema o la disciplina en la que se aplican, y pueden variar de un contexto a otro.

En general, los axiomas se establecen a partir de la observación empírica, la intuición y la experiencia acumulada en la disciplina en cuestión. Por ejemplo, en la geometría euclidiana, los axiomas se basan en la observación de los objetos y las relaciones espaciales en el mundo real, y en la intuición que tenemos sobre la geometría.

En otras disciplinas, como la lógica formal, los axiomas se establecen a partir de la definición de los conceptos fundamentales y las reglas que rigen su uso. Por ejemplo, en la lógica proposicional, los axiomas son enunciados que expresan las reglas básicas de la negación, la conjunción y la disyunción, y a partir de ellos se construye todo el sistema lógico.

La importancia de los axiomas en la lógica y la matemática

Los axiomas son fundamentales en la lógica y la matemática, ya que proporcionan la base sólida sobre la que se construyen los sistemas lógicos y matemáticos. Sin ellos, no sería posible establecer la validez de las proposiciones y los argumentos, y no podríamos desarrollar teoremas y demostraciones que permitan avanzar en la disciplina.

Además, los axiomas también son importantes porque permiten establecer los límites y las condiciones de aplicación de una disciplina. Por ejemplo, en la geometría euclidiana, los axiomas establecen las condiciones bajo las cuales se pueden establecer las propiedades de los objetos geométricos, y en la lógica formal, los axiomas establecen las reglas que rigen el uso de los conceptos básicos.

Cómo se utilizan los axiomas en la lógica y la matemática

En la lógica y la matemática, los axiomas se utilizan como base para la construcción de sistemas lógicos y matemáticos sólidos. A partir de ellos, se deducen los teoremas y las demostraciones que permiten establecer la validez de las proposiciones y los argumentos.

En la lógica proposicional, por ejemplo, los axiomas se utilizan para establecer las reglas básicas de la negación, la conjunción y la disyunción, y a partir de ellos se construyen las tablas de verdad y las demostraciones que permiten establecer la validez de las proposiciones.

En la geometría euclidiana, los axiomas se utilizan para establecer las propiedades de los objetos geométricos, como la congruencia, la semejanza y la perpendicularidad, y a partir de ellos se construyen las demostraciones que permiten establecer los teoremas.

Conclusión

Los axiomas son la base de la lógica y la matemática, y proporcionan la base sólida sobre la que se construyen los sistemas lógicos y matemáticos. Se establecen a partir de la observación empírica, la intuición y la experiencia acumulada en la disciplina en cuestión, y se utilizan para establecer la validez de las proposiciones y los argumentos.

Preguntas frecuentes

1. ¿Todos los sistemas lógicos y matemáticos tienen los mismos axiomas?

No necesariamente. Los axiomas pueden variar de un sistema a otro, dependiendo del contexto en el que se aplican. Por ejemplo, los axiomas de la geometría euclidiana son diferentes de los axiomas de la geometría no euclidiana.

2. ¿Qué sucede si un axioma resulta ser falso?

Si un axioma resulta ser falso, se debe revisar todo el sistema lógico o matemático en el que se aplica, ya que esto puede afectar la validez de los teoremas y las demostraciones que se derivan de él.

3. ¿Qué sucede si no se pueden establecer axiomas para una disciplina?

Si no se pueden establecer axiomas para una disciplina, es posible que no se pueda desarrollar un sistema lógico o matemático sólido para ella, o que se deba buscar una base diferente para construirlo.

4. ¿Los axiomas son siempre verdaderos?

Los axiomas se consideran verdaderos por definición, sin necesidad de demostración previa. Sin embargo, esto no significa que sean verdaderos en el sentido empírico o ontológico.

5. ¿Los axiomas pueden cambiar con el tiempo?

Sí, los axiomas pueden cambiar con el tiempo, dependiendo de los avances y los descubrimientos en la disciplina en cuestión. Por ejemplo, los axiomas de la física han evolucionado a lo largo del tiempo a medida que se han descubierto nuevas leyes y principios.