Descubre qué es una función constante y cómo identificarla

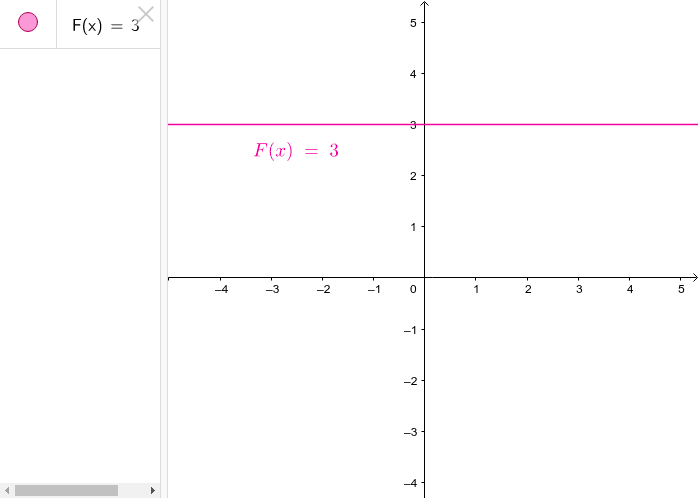
Si estás estudiando matemáticas, seguramente habrás oído hablar de las funciones constantes. Pero, ¿qué son exactamente y cómo podemos identificarlas? En este artículo vamos a explicar de forma clara y sencilla qué es una función constante y cómo podemos reconocerla.

¿Qué es una función constante?

Una función constante es una función matemática en la que el valor de la salida o resultado es siempre el mismo, independientemente del valor de la entrada. Esto significa que si x es cualquier número real, la función siempre dará como resultado el mismo número.

Por ejemplo, la función f(x) = 3 es una función constante, ya que independientemente del valor de x que introduzcamos, el resultado siempre será 3. Otras funciones constantes pueden ser f(x) = -4, f(x) = 0 o f(x) = 7. Todas ellas tienen en común que el resultado siempre es el mismo, sin importar el valor de x.

Cómo identificar una función constante

Para identificar una función constante, lo único que tenemos que hacer es fijarnos en la expresión matemática que la define. Si la función tiene la forma f(x) = c, donde c es un número constante, entonces se trata de una función constante.

Veamos algunos ejemplos:

- f(x) = 5x - 5 no es una función constante, ya que el resultado depende del valor de x.
- f(x) = 3 es una función constante, ya que el resultado siempre es 3, independientemente del valor de x.
- f(x) = -1/2 es otra función constante, ya que el resultado siempre es -1/2, sin importar el valor de x.

Propiedades de las funciones constantes

Las funciones constantes tienen algunas propiedades que las hacen interesantes desde el punto de vista matemático. Algunas de ellas son las siguientes:

- La gráfica de una función constante es una línea horizontal paralela al eje de las x. Esta línea corta al eje de las y en el valor que define la constante.
- La pendiente de una función constante es siempre cero, ya que la función no varía su resultado aunque se varíe la entrada x.
- El dominio de una función constante es el conjunto de todos los números reales, ya que no hay restricciones sobre qué valores de x pueden ser introducidos en la función.

Ejemplos de funciones constantes

Veamos algunos ejemplos de funciones constantes y cómo podemos identificarlas:

- f(x) = 6. En este caso, el valor de la función siempre es 6, independientemente del valor de x. Por lo tanto, se trata de una función constante.
- g(x) = 2x + 3. En este caso, el valor de la función depende del valor de x. Por lo tanto, no se trata de una función constante.
- h(x) = -2. En este caso, el valor de la función siempre es -2, sin importar el valor de x. Por lo tanto, se trata de una función constante.

Conclusión

Una función constante es una función matemática en la que el valor de la salida o resultado es siempre el mismo, independientemente del valor de la entrada. Para identificar una función constante, debemos fijarnos en la expresión matemática y comprobar si tiene la forma f(x) = c, donde c es un número constante. Las funciones constantes tienen propiedades interesantes, como una gráfica horizontal y una pendiente cero.

Preguntas frecuentes

1. ¿Todas las funciones que tienen una constante son funciones constantes?

No necesariamente. Una función puede tener una constante como parte de su expresión matemática, pero si el resultado de la función varía en función del valor de la entrada, no se trata de una función constante.

2. ¿Las funciones constantes son útiles en matemáticas?

Aunque parezca que las funciones constantes no tienen mucha utilidad, en realidad son importantes en algunos cálculos matemáticos. Además, son una herramienta útil para entender mejor el concepto de función y sus propiedades.

3. ¿Las funciones lineales son siempre funciones constantes?

No necesariamente. Las funciones lineales tienen la forma f(x) = mx + b, donde m y b son constantes. Si m es igual a cero, entonces la función es constante, pero si m es distinto de cero, la función no es constante.

4. ¿Es posible que una función constante tenga más de una variable?

Sí, es posible. En ese caso, la función tendría la forma f(x, y, z) = c, donde c es una constante y x, y, z son variables independientes. El valor de la función seguiría siendo siempre el mismo, independientemente de los valores de las variables.

5. ¿Las funciones constantes pueden ser negativas?

Sí, las funciones constantes pueden ser cualquier número real, positivo o negativo. Lo importante es que el valor de la función sea siempre el mismo, independientemente del valor de la entrada.