Descubre los tipos de teoremas: ¡Domina la matemática!

La matemática es una disciplina que puede intimidar a muchas personas, pero con la práctica y el conocimiento adecuado, puede ser una materia fascinante y satisfactoria. Uno de los aspectos más importantes de la matemática es la comprensión de los teoremas, que son proposiciones matemáticas que se han demostrado ser verdaderas en un amplio rango de situaciones.

Los teoremas son una parte fundamental de la matemática y se utilizan en una amplia variedad de campos, desde la física y la ingeniería hasta la economía y la informática. En este artículo, vamos a explorar los diferentes tipos de teoremas que existen y cómo pueden ayudarnos a entender mejor la matemática.

Tipos de Teoremas

Teoremas Geométricos

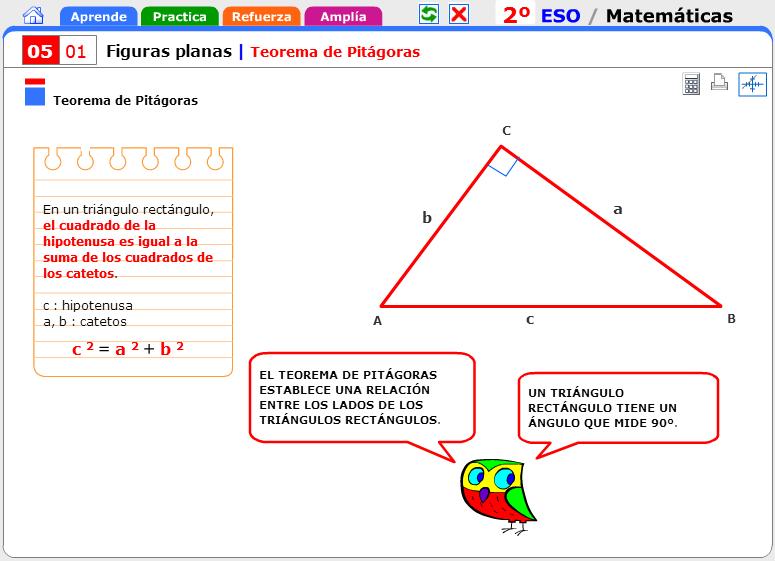
Los teoremas geométricos son aquellos que se relacionan con la geometría, la rama de las matemáticas que estudia las propiedades y relaciones de los objetos en el espacio. Ejemplos de teoremas geométricos son el teorema de Pitágoras, que establece la relación entre los lados de un triángulo rectángulo, y el teorema de Thales, que afirma que si dos triángulos son similares, entonces las longitudes de sus lados son proporcionales.

Teoremas de Álgebra

Los teoremas de álgebra se centran en las propiedades de las operaciones matemáticas, como la suma, la multiplicación y la división. Un ejemplo de teorema de álgebra es el teorema fundamental del álgebra, que establece que todo polinomio complejo de grado n tiene n raíces complejas distintas.

Teoremas de Análisis

Los teoremas de análisis son aquellos que se relacionan con el cálculo y el análisis matemático. Estos teoremas se utilizan para estudiar las propiedades de las funciones, como su continuidad, su derivabilidad y su integrabilidad. Ejemplos de teoremas de análisis incluyen el teorema del valor medio, que establece que para cualquier función continua en un intervalo dado, existe al menos un punto en ese intervalo donde la pendiente de la recta tangente a la función es igual a la pendiente de la recta secante que une los extremos del intervalo.

Teoremas de Probabilidad

Los teoremas de probabilidad se utilizan para estudiar el comportamiento de los eventos aleatorios y de las distribuciones de probabilidad. Ejemplos de teoremas de probabilidad incluyen el teorema de Bayes, que establece la relación entre la probabilidad de un evento y la probabilidad condicionada de ese evento dado otro evento relacionado, y el teorema del límite central, que establece que la distribución de la media de una muestra aleatoria de una población se aproxima a una distribución normal a medida que el tamaño de la muestra aumenta.

Teoremas de Combinatoria

Los teoremas de combinatoria se utilizan para estudiar la combinación de objetos y eventos. Ejemplos de teoremas de combinatoria incluyen el teorema del binomio, que establece la expansión del binomio (a + b) elevado a una potencia n, y el teorema de Vandermonde, que establece la relación entre los coeficientes binomiales.

Conclusión

Los teoremas son una parte fundamental de la matemática y se utilizan en una amplia variedad de campos. Comprender los diferentes tipos de teoremas puede ayudarnos a entender mejor la matemática y a aplicarla de manera efectiva en nuestras vidas. Ya sea en la física, la economía o la informática, los teoremas son una herramienta poderosa para resolver problemas y tomar decisiones informadas.

Preguntas Frecuentes

¿Cómo se demuestran los teoremas?

Los teoremas se demuestran utilizando la lógica matemática y las propiedades de los números y las funciones. La demostración de un teorema implica establecer una serie de pasos lógicos que muestran que la proposición es verdadera en todas las situaciones.

¿Qué es un corolario?

Un corolario es una proposición que se deriva de un teorema y que se considera una consecuencia directa del teorema original. Los corolarios son útiles porque permiten aplicar las conclusiones de un teorema a situaciones específicas.

¿Qué es un axioma?

Un axioma es una proposición que se considera verdadera sin necesidad de demostración. Los axiomas se utilizan como base para la construcción de teoremas y otras proposiciones matemáticas.

¿Cómo se utilizan los teoremas en la vida cotidiana?

Los teoremas se utilizan en la vida cotidiana en una amplia variedad de situaciones, desde el diseño de estructuras y la resolución de problemas de ingeniería hasta la toma de decisiones financieras y la interpretación de datos científicos. Comprender los teoremas puede ayudarnos a tomar decisiones informadas y resolver problemas de manera efectiva.

¿Por qué es importante conocer los teoremas?

Los teoremas son importantes porque nos permiten entender mejor la matemática y aplicarla de manera efectiva en nuestras vidas. Comprender los teoremas nos ayuda a resolver problemas de manera efectiva, tomar decisiones informadas y comprender mejor el mundo que nos rodea.