Descubre los tipos de proposiciones en matemáticas

Las proposiciones son afirmaciones que pueden ser verdaderas o falsas, y en matemáticas, son fundamentales para la construcción de teoremas y demostraciones. En este artículo, descubrirás los diferentes tipos de proposiciones en matemáticas y cómo se utilizan en el razonamiento matemático.

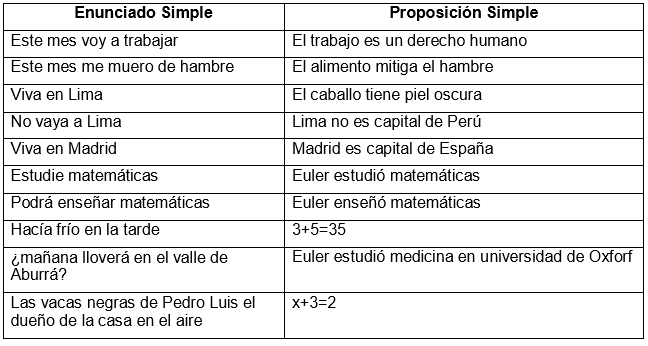
Proposiciones simples

Las proposiciones simples son las afirmaciones más básicas que se pueden hacer en matemáticas, y se pueden expresar en términos de verdadero o falso. Por ejemplo, "2+2=4" es una proposición simple que es verdadera, mientras que "3+5=10" es una proposición simple que es falsa.

Proposiciones compuestas

Las proposiciones compuestas se crean a partir de proposiciones simples utilizando conectores lógicos como "y", "o" y "no". Por ejemplo, "3 es un número impar y 5 es un número primo" es una proposición compuesta que es verdadera, ya que ambas proposiciones simples son verdaderas. Por otro lado, "2+2=5 o 3+3=7" es una proposición compuesta que es falsa, ya que ambas proposiciones simples son falsas.

Proposiciones condicionales

Las proposiciones condicionales son una forma de proposición compuesta que se expresa como "si p entonces q", donde p y q son afirmaciones. Por ejemplo, "si x es un número par, entonces x+2 también es un número par" es una proposición condicional que es verdadera.

Proposiciones bicondicionales

Las proposiciones bicondicionales son una forma de proposición compuesta que se expresa como "p si y solo si q", donde p y q son afirmaciones. Por ejemplo, "un triángulo es equilátero si y solo si sus tres lados tienen la misma longitud" es una proposición bicondicional que es verdadera.

Proposiciones cuantificadas

Las proposiciones cuantificadas se utilizan para expresar afirmaciones sobre conjuntos de objetos. Por ejemplo, "para todo número entero n, existe otro número entero m tal que n+m=0" es una proposición cuantificada que es verdadera para todos los números enteros.

Proposiciones existenciales

Las proposiciones existenciales se utilizan para afirmar la existencia de objetos con ciertas propiedades. Por ejemplo, "existe un número entero n tal que n es divisible por 4" es una proposición existencial que es verdadera, ya que podemos encontrar un número entero que cumpla esta propiedad.

Conclusión

Las proposiciones son elementos fundamentales del razonamiento matemático y se utilizan para construir teoremas y demostraciones. Los diferentes tipos de proposiciones en matemáticas incluyen proposiciones simples, proposiciones compuestas, proposiciones condicionales, proposiciones bicondicionales, proposiciones cuantificadas y proposiciones existenciales.

Preguntas frecuentes

1. ¿Qué es una proposición en matemáticas?

Una proposición en matemáticas es una afirmación que puede ser verdadera o falsa.

2. ¿Por qué son importantes las proposiciones en matemáticas?

Las proposiciones son importantes en matemáticas porque se utilizan para construir teoremas y demostraciones.

3. ¿Cómo se crean las proposiciones compuestas?

Las proposiciones compuestas se crean a partir de proposiciones simples utilizando conectores lógicos como "y", "o" y "no".

4. ¿Qué son las proposiciones condicionales?

Las proposiciones condicionales son una forma de proposición compuesta que se expresa como "si p entonces q", donde p y q son afirmaciones.

5. ¿Qué son las proposiciones cuantificadas?

Las proposiciones cuantificadas se utilizan para expresar afirmaciones sobre conjuntos de objetos.