Descubre los tipos de proposiciones en lógica matemática
La lógica matemática es una rama de las matemáticas que se encarga de estudiar la estructura y el razonamiento de los argumentos en términos formales. Una de las bases de la lógica matemática son las proposiciones, que son enunciados que pueden ser verdaderos o falsos. En este artículo, descubriremos los diferentes tipos de proposiciones en lógica matemática.
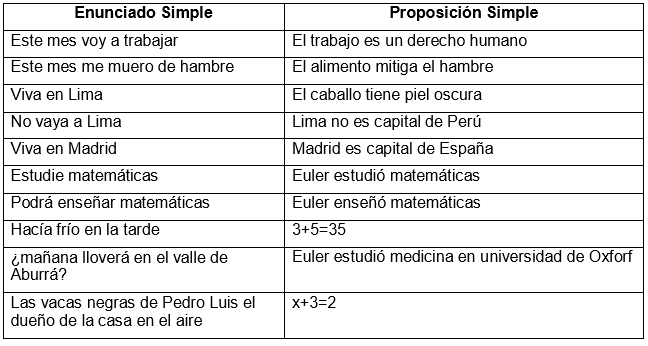
Proposiciones simples
Las proposiciones simples son enunciados que no contienen ninguna otra proposición dentro de ellas. Por ejemplo, el enunciado "2 + 2 = 4" es una proposición simple, ya que no contiene ninguna otra proposición dentro de ella. Las proposiciones simples pueden ser verdaderas o falsas, pero nunca ambas a la vez.
Proposiciones compuestas
Las proposiciones compuestas son enunciados que están formados por dos o más proposiciones simples unidas por conectores lógicos. Los conectores lógicos más comunes son "y", "o" y "no". Por ejemplo, el enunciado "2 + 2 = 4 y 3 + 3 = 6" es una proposición compuesta, ya que está formada por dos proposiciones simples unidas por el conector lógico "y".
Proposiciones conjuntivas
Las proposiciones conjuntivas son proposiciones compuestas que están formadas por dos o más proposiciones simples unidas por el conector lógico "y". Por ejemplo, el enunciado "Juan estudia matemáticas y María estudia física" es una proposición conjuntiva, ya que está formada por dos proposiciones simples unidas por el conector lógico "y".
Proposiciones disyuntivas
Las proposiciones disyuntivas son proposiciones compuestas que están formadas por dos o más proposiciones simples unidas por el conector lógico "o". Por ejemplo, el enunciado "Si llueve, me quedo en casa o si hace sol, voy a la playa" es una proposición disyuntiva, ya que está formada por dos proposiciones simples unidas por el conector lógico "o".
Proposiciones condicionales
Las proposiciones condicionales son proposiciones compuestas que están formadas por dos proposiciones simples unidas por el conector lógico "si...entonces". Por ejemplo, el enunciado "Si estudio, aprobaré el examen" es una proposición condicional, ya que está formada por dos proposiciones simples unidas por el conector lógico "si...entonces".
Proposiciones bicondicionales
Las proposiciones bicondicionales son proposiciones compuestas que están formadas por dos proposiciones simples unidas por el conector lógico "si y solo si". Por ejemplo, el enunciado "Un triángulo es equilátero si y solo si sus tres lados son iguales" es una proposición bicondicional, ya que está formada por dos proposiciones simples unidas por el conector lógico "si y solo si".
Conclusión
La lógica matemática se basa en el estudio de las proposiciones, que son enunciados que pueden ser verdaderos o falsos. Existen diferentes tipos de proposiciones en lógica matemática, como las proposiciones simples y las proposiciones compuestas. Las proposiciones compuestas pueden ser conjuntivas, disyuntivas, condicionales o bicondicionales, dependiendo del conector lógico que las una.
Preguntas frecuentes
1. ¿Qué es una proposición en lógica matemática?
Una proposición en lógica matemática es un enunciado que puede ser verdadero o falso.
2. ¿Qué son las proposiciones simples?
Las proposiciones simples son enunciados que no contienen ninguna otra proposición dentro de ellas.
3. ¿Cuáles son los conectores lógicos más comunes en lógica matemática?
Los conectores lógicos más comunes en lógica matemática son "y", "o" y "no".
4. ¿Qué son las proposiciones condicionales?
Las proposiciones condicionales son proposiciones compuestas que están formadas por dos proposiciones simples unidas por el conector lógico "si...entonces".
5. ¿Qué son las proposiciones bicondicionales?
Las proposiciones bicondicionales son proposiciones compuestas que están formadas por dos proposiciones simples unidas por el conector lógico "si y solo si".
Deja una respuesta