Descubre los tipos de conjunto: finitos, infinitos y más
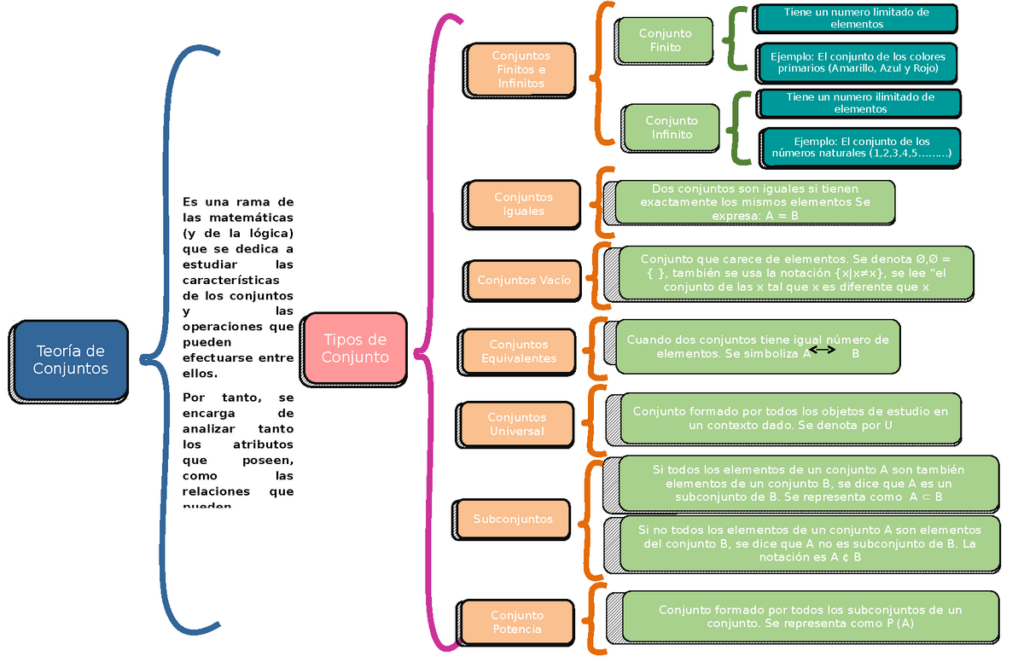
Si estás estudiando matemáticas, es muy probable que hayas escuchado hablar sobre conjuntos. Los conjuntos son una herramienta fundamental en el ámbito de las matemáticas y se utilizan para representar una colección de objetos o elementos. En este artículo, descubrirás los tipos de conjuntos existentes, desde los finitos hasta los infinitos y más.
¿Qué es un conjunto?
Un conjunto es una colección de elementos que comparten una característica en común. Por ejemplo, el conjunto de los números pares es una colección de números que son divisibles por dos. Los elementos de un conjunto pueden ser números, letras, palabras, objetos, entre otros.
Tipos de conjuntos
Existen diferentes tipos de conjuntos, desde los más simples hasta los más complejos. A continuación, te mostramos los tipos de conjuntos más comunes:
1. Conjuntos finitos
Los conjuntos finitos son aquellos que tienen un número limitado de elementos. Por ejemplo, el conjunto de los días de la semana es un conjunto finito, ya que solo tiene siete elementos: lunes, martes, miércoles, jueves, viernes, sábado y domingo.
2. Conjuntos infinitos
Los conjuntos infinitos son aquellos que tienen una cantidad infinita de elementos. Por ejemplo, el conjunto de los números naturales es un conjunto infinito, ya que no existe un número límite de elementos.
3. Conjuntos vacíos
Los conjuntos vacíos son aquellos que no tienen ningún elemento. Por ejemplo, el conjunto de los números negativos mayores a 0 es un conjunto vacío, ya que no existen números que cumplan con esa característica.
4. Conjuntos unitarios
Los conjuntos unitarios son aquellos que tienen un solo elemento. Por ejemplo, el conjunto {2} es un conjunto unitario, ya que solo tiene el elemento 2.
5. Conjuntos complementarios
Los conjuntos complementarios son aquellos que contienen todos los elementos que no están en otro conjunto. Por ejemplo, si tenemos el conjunto A = {1, 2, 3} y el conjunto universal U = {1, 2, 3, 4, 5}, el conjunto complementario de A es U - A = {4, 5}.
6. Conjuntos disjuntos
Los conjuntos disjuntos son aquellos que no tienen elementos en común. Por ejemplo, si tenemos el conjunto A = {1, 2, 3} y el conjunto B = {4, 5, 6}, estos conjuntos son disjuntos ya que no comparten ningún elemento.
7. Conjuntos equivalentes
Los conjuntos equivalentes son aquellos que tienen la misma cantidad de elementos. Por ejemplo, el conjunto A = {1, 2, 3} y el conjunto B = {4, 5, 6} no son equivalentes, pero el conjunto C = {1, 2, 3} y el conjunto D = {3, 2, 1} sí son equivalentes, ya que ambos tienen tres elementos.
8. Conjuntos ordenados
Los conjuntos ordenados son aquellos en los que importa el orden en el que se presentan los elementos. Por ejemplo, el conjunto A = {1, 2, 3} y el conjunto B = {3, 2, 1} son diferentes conjuntos ordenados, ya que el orden en el que se presentan los elementos es diferente.
Conclusión
Los conjuntos son una herramienta fundamental en las matemáticas y existen diferentes tipos de conjuntos, desde los finitos hasta los infinitos y más. Es importante conocer cada uno de ellos para poder aplicarlos correctamente en diferentes situaciones.
Preguntas frecuentes
1. ¿Qué es un conjunto?
Un conjunto es una colección de elementos que comparten una característica en común.
2. ¿Qué es un conjunto finito?
Un conjunto finito es aquel que tiene un número limitado de elementos.
3. ¿Qué es un conjunto infinito?
Un conjunto infinito es aquel que tiene una cantidad infinita de elementos.
4. ¿Qué es un conjunto vacío?
Un conjunto vacío es aquel que no tiene ningún elemento.
5. ¿Qué es un conjunto complementario?
Un conjunto complementario es aquel que contiene todos los elementos que no están en otro conjunto.
Deja una respuesta