Descubre los teoremas fundamentales de Álgebra Booleana
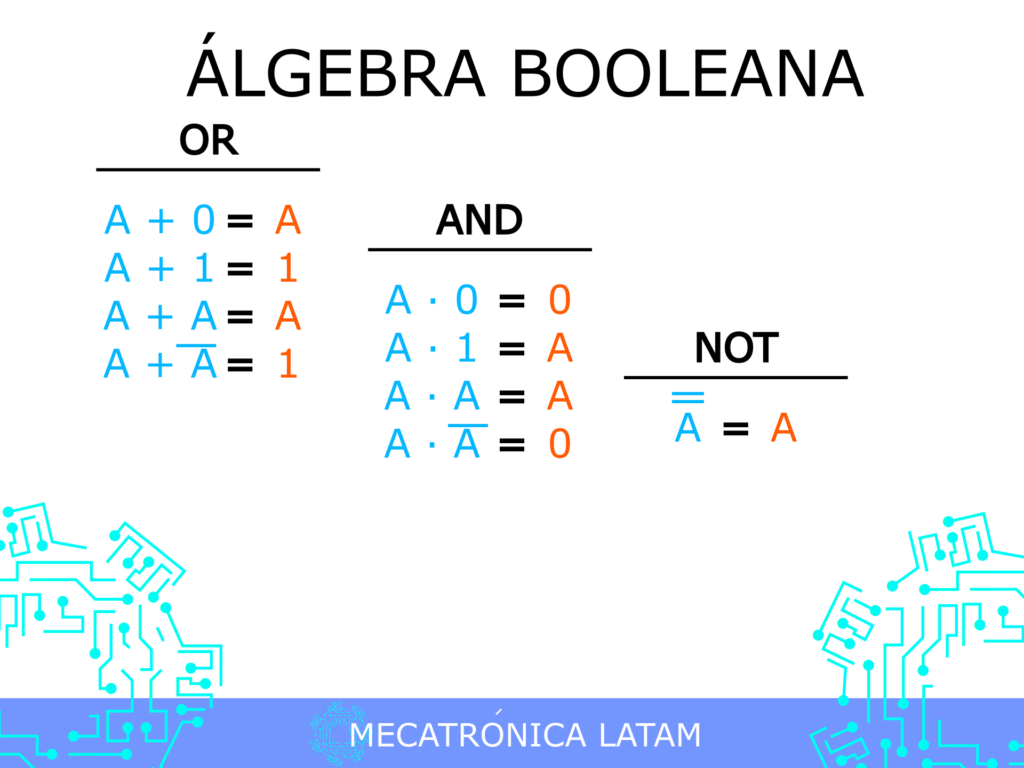
Si eres un estudiante de matemáticas o ciencias de la computación, seguramente hayas escuchado hablar de Álgebra Booleana. Esta rama de las matemáticas se enfoca en el estudio de operaciones lógicas y cómo se aplican en los sistemas digitales. En este artículo, vamos a profundizar en los teoremas fundamentales de Álgebra Booleana y cómo se utilizan en la tecnología moderna.
- ¿Qué es el Álgebra Booleana?
- Los Teoremas fundamentales de Álgebra Booleana
- Aplicaciones de Álgebra Booleana
- Conclusión
-
Preguntas frecuentes
- 1. ¿Qué es el Álgebra Booleana?
- 2. ¿Quién desarrolló el Álgebra Booleana?
- 3. ¿Cómo se utilizan los teoremas de Álgebra Booleana en la programación de computadoras?
- 4. ¿Cómo se utilizan los teoremas de Álgebra Booleana en la criptografía?
- 5. ¿Por qué es importante comprender los teoremas de Álgebra Booleana?
¿Qué es el Álgebra Booleana?
El Álgebra Booleana es una rama de las matemáticas que se enfoca en el estudio de operaciones lógicas y cómo se aplican en los sistemas digitales. Fue desarrollada por George Boole en el siglo XIX, y desde entonces ha sido utilizada en la tecnología moderna, particularmente en la electrónica digital y la informática.
El Álgebra Booleana se basa en la teoría de conjuntos y en la lógica proposicional, y utiliza operaciones lógicas como AND, OR y NOT para manipular valores binarios (0 y 1).
Los Teoremas fundamentales de Álgebra Booleana
Los Teoremas fundamentales de Álgebra Booleana son reglas matemáticas que se utilizan para simplificar y manipular expresiones booleanas. Estos teoremas son la base para el diseño y análisis de circuitos digitales, y son esenciales para la programación de computadoras.
Teorema de la Identidad
El Teorema de la Identidad establece que cualquier operando booleano combinado con un elemento neutro (0 o 1) resulta en el mismo operando. Por ejemplo:
A + 0 = A
A * 1 = A
Este teorema es útil para simplificar operaciones booleanas y reducir el número de términos.
Teorema de la Complementación
El Teorema de la Complementación establece que el complemento de un operando booleano es igual a su negación. Por ejemplo:
A + ~A = 1
A * ~A = 0
Este teorema es útil para simplificar operaciones booleanas y reducir el número de términos.
Teorema de la Simplificación
El Teorema de la Simplificación establece que cualquier término booleano combinado con su complemento resulta en 0. Por ejemplo:
A + ~A * B = A * B
Este teorema es útil para simplificar operaciones booleanas y reducir el número de términos.
Teorema de la Distribución
El Teorema de la Distribución establece que cualquier término booleano distribuido sobre una operación AND o OR resulta en una expresión equivalente. Por ejemplo:
A * (B + C) = A * B + A * C
A + (B * C) = (A + B) * (A + C)
Este teorema es útil para simplificar operaciones booleanas y reducir el número de términos.
Teorema de la Asociatividad
El Teorema de la Asociatividad establece que cualquier operación AND o OR se puede asociar de manera diferente sin afectar el resultado final. Por ejemplo:
(A * B) * C = A * (B * C)
(A + B) + C = A + (B + C)
Este teorema es útil para simplificar operaciones booleanas y reducir el número de términos.
Aplicaciones de Álgebra Booleana
El Álgebra Booleana se utiliza en una amplia variedad de aplicaciones, desde el diseño de circuitos digitales hasta la programación de computadoras. Algunos ejemplos de su uso incluyen:
- Diseño de circuitos lógicos: El Álgebra Booleana se utiliza para simplificar y analizar circuitos digitales, lo que ayuda a los ingenieros a diseñar sistemas más eficientes y confiables.
- Programación de computadoras: El Álgebra Booleana se utiliza para crear expresiones lógicas en programas de computadoras, lo que permite a los desarrolladores crear programas más sofisticados y eficientes.
- Criptografía: El Álgebra Booleana se utiliza en la criptografía para garantizar la seguridad de los datos. Los algoritmos criptográficos utilizan operaciones booleanas para cifrar y descifrar información.
Conclusión
Los Teoremas fundamentales de Álgebra Booleana son esenciales para el diseño y análisis de circuitos digitales, y son una parte fundamental de la tecnología moderna. La comprensión de estos teoremas es esencial para cualquier estudiante de matemáticas o ciencias de la computación que quiera trabajar en el campo de la electrónica digital y la informática.
Preguntas frecuentes
1. ¿Qué es el Álgebra Booleana?
El Álgebra Booleana es una rama de las matemáticas que se enfoca en el estudio de operaciones lógicas y cómo se aplican en los sistemas digitales.
2. ¿Quién desarrolló el Álgebra Booleana?
El Álgebra Booleana fue desarrollada por George Boole en el siglo XIX.
3. ¿Cómo se utilizan los teoremas de Álgebra Booleana en la programación de computadoras?
Los teoremas de Álgebra Booleana se utilizan para crear expresiones lógicas en programas de computadoras, lo que permite a los desarrolladores crear programas más sofisticados y eficientes.
4. ¿Cómo se utilizan los teoremas de Álgebra Booleana en la criptografía?
Los teoremas de Álgebra Booleana se utilizan en la criptografía para garantizar la seguridad de los datos. Los algoritmos criptográficos utilizan operaciones booleanas para cifrar y descifrar información.
5. ¿Por qué es importante comprender los teoremas de Álgebra Booleana?
La comprensión de los teoremas de Álgebra Booleana es esencial para cualquier estudiante de matemáticas o ciencias de la computación que quiera trabajar en el campo de la electrónica digital y la informática. Estos teoremas son la base para el diseño y análisis de circuitos digitales, y son una parte fundamental de la tecnología moderna.
Deja una respuesta