Descubre los 5 tipos de operaciones con conjuntos
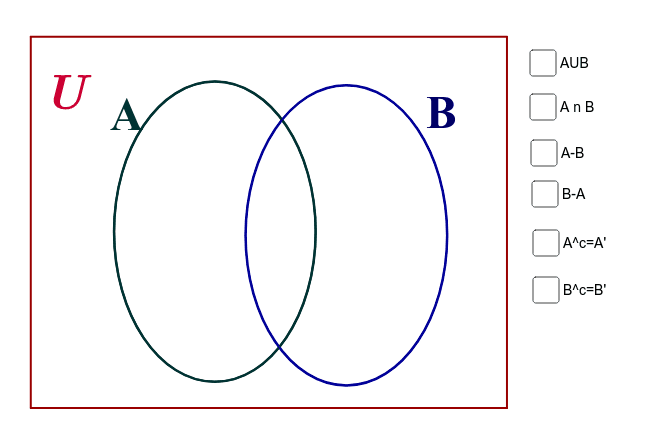
Los conjuntos son un concepto matemático fundamental que se utiliza en diversas áreas de la ciencia y la tecnología. Los conjuntos son colecciones de objetos que pueden ser números, letras, palabras, entre otros. En este artículo, vamos a descubrir los 5 tipos de operaciones con conjuntos más importantes que debes conocer.
1. Unión de conjuntos
La unión de conjuntos se refiere a la combinación de dos o más conjuntos en uno solo. Para realizar esta operación, se deben tomar todos los elementos de los conjuntos involucrados y colocarlos en un nuevo conjunto. Si hay elementos repetidos, se eliminan para que el conjunto resultante tenga elementos únicos. La unión de conjuntos se representa con el símbolo "∪".
Por ejemplo, si tenemos dos conjuntos A = {1, 2, 3} y B = {3, 4, 5}, la unión de A y B sería: A ∪ B = {1, 2, 3, 4, 5}
2. Intersección de conjuntos
La intersección de conjuntos se refiere a la búsqueda de los elementos que dos o más conjuntos tienen en común. Para realizar esta operación, se deben comparar los elementos de los conjuntos involucrados y colocar los elementos compartidos en un nuevo conjunto. La intersección de conjuntos se representa con el símbolo "∩".
Por ejemplo, si tenemos dos conjuntos A = {1, 2, 3} y B = {3, 4, 5}, la intersección de A y B sería: A ∩ B = {3}
3. Diferencia de conjuntos
La diferencia de conjuntos se refiere a la eliminación de los elementos de un conjunto que también se encuentran en otro conjunto. Para realizar esta operación, se deben tomar los elementos del primer conjunto y eliminar los elementos que se encuentran en el segundo conjunto. La diferencia de conjuntos se representa con el símbolo "-".
Por ejemplo, si tenemos dos conjuntos A = {1, 2, 3} y B = {3, 4, 5}, la diferencia de A y B sería: A - B = {1, 2}
4. Complemento de un conjunto
El complemento de un conjunto se refiere a los elementos que no se encuentran en un conjunto. Esta operación se realiza en relación a un conjunto universo, que es el conjunto que contiene todos los elementos posibles. El complemento de un conjunto se representa con el símbolo "C".
Por ejemplo, si tenemos un conjunto A = {1, 2, 3} y un conjunto universo U = {1, 2, 3, 4, 5}, el complemento de A sería: A^C = {4, 5}
5. Producto cartesiano de conjuntos
El producto cartesiano de dos conjuntos se refiere a la combinación de todos los elementos de los conjuntos involucrados. Para realizar esta operación, se deben tomar cada elemento del primer conjunto y combinarlo con todos los elementos del segundo conjunto. El producto cartesiano de conjuntos se representa con el símbolo "x".
Por ejemplo, si tenemos dos conjuntos A = {1, 2} y B = {a, b}, el producto cartesiano de A y B sería: A x B = {(1, a), (1, b), (2, a), (2, b)}
Conclusión
Los conjuntos y sus operaciones son un concepto fundamental en la matemática y en diversas áreas de la ciencia y la tecnología. La unión, intersección, diferencia, complemento y producto cartesiano son los cinco tipos de operaciones con conjuntos más importantes que debes conocer.
Preguntas frecuentes
¿Qué es un conjunto?
Un conjunto es una colección de objetos que pueden ser números, letras, palabras, entre otros.
¿Qué es la unión de conjuntos?
La unión de conjuntos se refiere a la combinación de dos o más conjuntos en uno solo.
¿Cómo se representa la intersección de conjuntos?
La intersección de conjuntos se representa con el símbolo "∩".
¿Qué es el complemento de un conjunto?
El complemento de un conjunto se refiere a los elementos que no se encuentran en un conjunto.
¿Qué es el producto cartesiano de conjuntos?
El producto cartesiano de dos conjuntos se refiere a la combinación de todos los elementos de los conjuntos involucrados.
Deja una respuesta