Descubre los 5 teoremas de Thales y domina la geometría
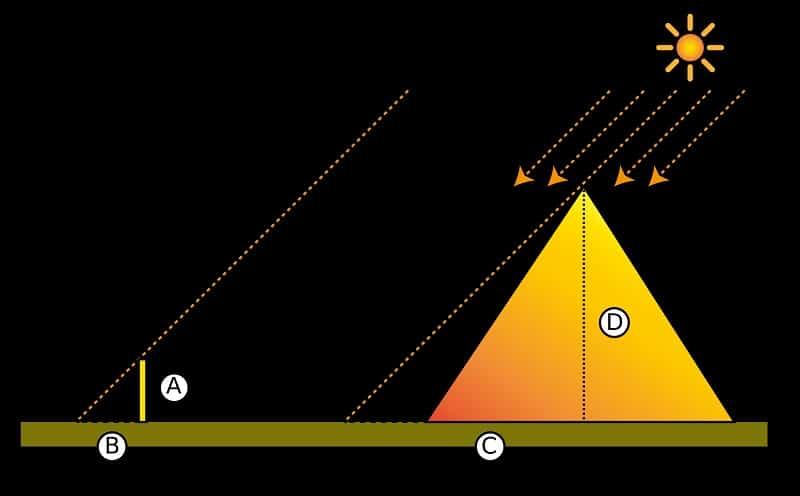
Si eres un estudiante de geometría, seguramente has escuchado hablar de los teoremas de Thales. Estos son fundamentales en el estudio de la geometría y son esenciales para dominar esta rama de las matemáticas. En este artículo, hablaremos sobre los 5 teoremas de Thales y cómo puedes utilizarlos para mejorar tus habilidades en geometría.
¿Quién fue Thales?
Antes de entrar en los teoremas de Thales, es importante conocer un poco sobre quién fue Thales. Thales de Mileto fue un filósofo, matemático y astrónomo de la antigua Grecia que vivió en el siglo VI a.C. Es conocido como uno de los Siete Sabios de Grecia y se le atribuyen varios descubrimientos matemáticos, incluyendo los teoremas que llevan su nombre.
¿Qué son los teoremas de Thales?
Los teoremas de Thales son un conjunto de cinco teoremas que se utilizan para resolver problemas de geometría. Estos teoremas están basados en la proporcionalidad y se utilizan para encontrar longitudes, ángulos y áreas en figuras geométricas.
Teorema 1: Teorema de la base media
El primer teorema de Thales es el teorema de la base media. Este teorema establece que si tienes un triángulo y trazas una línea paralela a uno de los lados que pase por el punto medio del otro lado, entonces esta línea dividirá al triángulo en dos triángulos de igual área.
Este teorema se basa en la proporcionalidad de los lados de los triángulos, lo que significa que si dos lados de un triángulo son iguales, las áreas de los triángulos formados por la línea paralela también son iguales.
Teorema 2: Teorema de la altura
El segundo teorema de Thales es el teorema de la altura. Este teorema establece que si tienes un triángulo y trazas una línea perpendicular desde un vértice al lado opuesto, entonces la longitud de esta línea es proporcional a la longitud del lado opuesto.
Este teorema es muy útil para encontrar la altura de un triángulo y se utiliza frecuentemente en cálculos de áreas.
Teorema 3: Teorema de la intersección
El tercer teorema de Thales es el teorema de la intersección. Este teorema establece que si tienes dos líneas paralelas y trazas una tercera línea que las intersecta, entonces los segmentos que se forman en la tercera línea son proporcionales.
Este teorema es muy útil para encontrar longitudes desconocidas en figuras geométricas que tienen líneas paralelas.
Teorema 4: Teorema de la bisectriz
El cuarto teorema de Thales es el teorema de la bisectriz. Este teorema establece que si tienes un triángulo y trazas una línea que biseca uno de los ángulos, entonces los lados del triángulo que forman este ángulo son proporcionales a los segmentos que se forman en la línea bisectriz.
Este teorema es muy útil para encontrar medidas desconocidas en triángulos y para resolver problemas de trigonometría.
Teorema 5: Teorema de Thales
El quinto y último teorema de Thales es el teorema de Thales propiamente dicho. Este teorema establece que si tienes dos triángulos que son semejantes, entonces los lados correspondientes son proporcionales.
Este teorema es muy útil para resolver problemas que involucran triángulos semejantes y para encontrar medidas desconocidas en figuras geométricas complejas.
Conclusión
Los teoremas de Thales son fundamentales en el estudio de la geometría y son esenciales para dominar esta rama de las matemáticas. Estos teoremas se basan en la proporcionalidad y se utilizan para encontrar longitudes, ángulos y áreas en figuras geométricas. Si eres un estudiante de geometría, es importante que domines estos teoremas para poder resolver problemas y aplicarlos en situaciones reales.
Preguntas frecuentes
1. ¿Por qué son importantes los teoremas de Thales?
Los teoremas de Thales son importantes porque se utilizan para resolver problemas de geometría y para encontrar medidas desconocidas en figuras geométricas. Estos teoremas son fundamentales en la geometría y son esenciales para dominar esta rama de las matemáticas.
2. ¿Cuál es el teorema más importante de Thales?
Todos los teoremas de Thales son importantes, pero el teorema de Thales propiamente dicho es el más fundamental. Este teorema establece que si tienes dos triángulos que son semejantes, entonces los lados correspondientes son proporcionales.
3. ¿Cómo puedo aplicar los teoremas de Thales en situaciones reales?
Los teoremas de Thales se pueden aplicar en situaciones reales para resolver problemas de geometría y para encontrar medidas desconocidas en figuras geométricas. Estos teoremas son útiles en arquitectura, ingeniería, diseño y muchas otras áreas que requieren conocimientos de geometría.
4. ¿Cómo puedo aprender más sobre los teoremas de Thales?
Puedes aprender más sobre los teoremas de Thales leyendo libros de geometría, asistiendo a clases de matemáticas o buscando información en línea. También puedes resolver problemas y ejercicios para practicar la aplicación de estos teoremas.
5. ¿Por qué Thales es considerado uno de los Siete Sabios de Grecia?
Thales es considerado uno de los Siete Sabios de Grecia por sus importantes contribuciones en filosofía, matemáticas y astronomía. Se le atribuyen varios descubrimientos matemáticos, incluyendo los teoremas que llevan su nombre, y se le considera uno de los padres de la ciencia y la filosofía occidentales.
Deja una respuesta