Descubre los 3 tipos de teoremas que debes conocer

Si eres un estudiante de matemáticas o simplemente te gusta aprender sobre esta disciplina, es importante que conozcas los diferentes tipos de teoremas que existen. En este artículo, te exploraremos los tres tipos de teoremas que debes conocer y cómo pueden ayudarte a comprender mejor la matemática.

Teoremas analíticos

Los teoremas analíticos se enfocan en la construcción de proposiciones matemáticas que se basan en la lógica y la razón. Estos teoremas son utilizados para demostrar la validez de una proposición matemática y se enfocan en la relación entre las variables y las funciones.

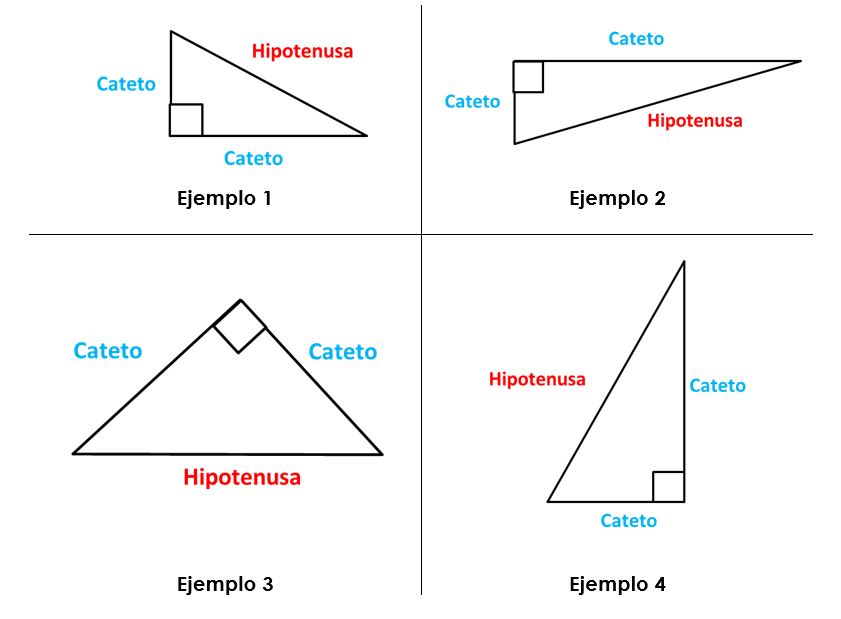
Un ejemplo de un teorema analítico es el teorema de Pitágoras. Este teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. Este teorema es considerado uno de los más importantes en la geometría y es utilizado en muchas aplicaciones prácticas.

Teoremas geométricos

Los teoremas geométricos se enfocan en el estudio de las formas y las figuras. Estos teoremas son utilizados para demostrar la validez de una proposición matemática y se enfocan en la relación entre las formas y las figuras.

Un ejemplo de un teorema geométrico es el teorema de Euclides. Este teorema establece que en un triángulo escaleno, las medianas de cualquier lado se intersectan en un punto común. Este teorema es utilizado en la geometría y en la construcción de estructuras arquitectónicas.

Teoremas algebraicos

Los teoremas algebraicos se enfocan en la relación entre las expresiones matemáticas y las ecuaciones. Estos teoremas son utilizados para demostrar la validez de una proposición matemática y se enfocan en la relación entre las expresiones matemáticas y las ecuaciones.

Un ejemplo de un teorema algebraico es el teorema fundamental del álgebra. Este teorema establece que cualquier polinomio de grado n tiene n raíces complejas únicas. Este teorema es utilizado en la álgebra y en la solución de ecuaciones polinómicas.

Conclusión

Los teoremas son importantes en la matemática porque nos permiten demostrar la validez de una proposición matemática. Los teoremas analíticos se enfocan en la construcción de proposiciones matemáticas que se basan en la lógica y la razón, los teoremas geométricos se enfocan en el estudio de las formas y las figuras, y los teoremas algebraicos se enfocan en la relación entre las expresiones matemáticas y las ecuaciones.

Preguntas frecuentes

¿Qué es un teorema?

Un teorema es una proposición matemática que ha sido demostrada como válida.

¿Por qué son importantes los teoremas en la matemática?

Los teoremas son importantes en la matemática porque nos permiten demostrar la validez de una proposición matemática.

¿Cuál es el teorema más importante en la geometría?

El teorema de Pitágoras es considerado uno de los teoremas más importantes en la geometría.

¿Cuál es el teorema más importante en el álgebra?

El teorema fundamental del álgebra es considerado uno de los teoremas más importantes en el álgebra.

¿Cuál es la diferencia entre un teorema analítico y un teorema geométrico?

Un teorema analítico se enfoca en la construcción de proposiciones matemáticas que se basan en la lógica y la razón, mientras que un teorema geométrico se enfoca en el estudio de las formas y las figuras.