Descubre los 3 teoremas de Tales: guía práctica
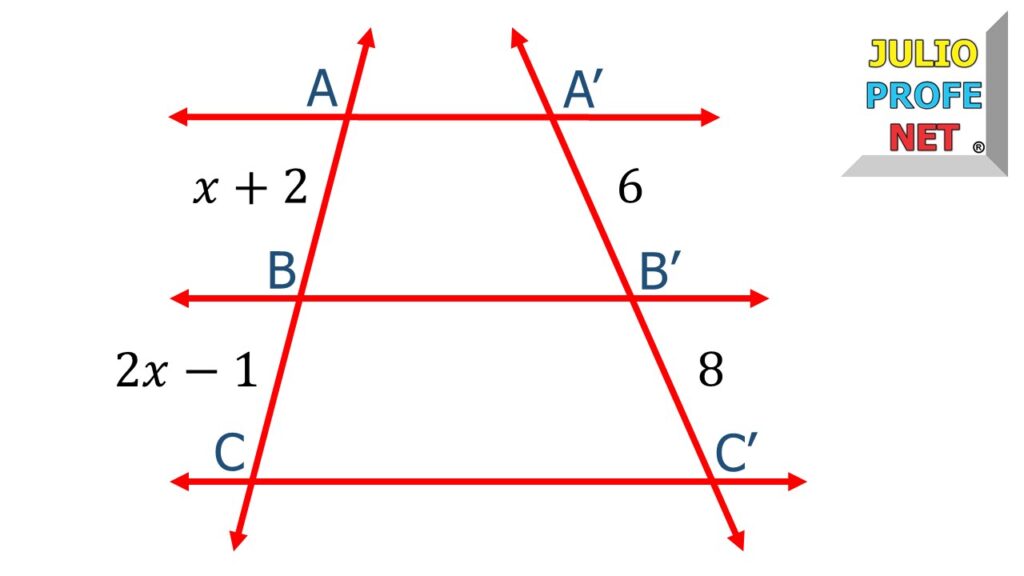
Los teoremas de Tales son fundamentales en la geometría, y se utilizan para resolver problemas de proporciones en triángulos y otras figuras geométricas. En este artículo, te presentamos una guía práctica que te ayudará a comprender los 3 teoremas de Tales.
¿Qué son los teoremas de Tales?
Los teoremas de Tales fueron descubiertos por el matemático griego Tales de Mileto en el siglo VI a.C. Estos teoremas establecen que si una serie de rectas paralelas cruzan a otras rectas, entonces las intersecciones de estas rectas paralelas crean segmentos que están en proporción.
Teorema de Tales
El primer teorema de Tales establece que si dos triángulos son semejantes, entonces las longitudes de los lados correspondientes son proporcionales. Esto significa que si tenemos dos triángulos ABC y A'B'C' que son semejantes, entonces:
AB/A'B' = BC/B'C' = AC/A'C'
Ejemplo:
Si tenemos dos triángulos semejantes, uno con lados de 6, 9 y 12 unidades y otro con lados de 4, 6 y 8 unidades, podemos usar el teorema de Tales para encontrar la proporción entre los lados correspondientes.
AB/A'B' = 6/4 = 3/2
BC/B'C' = 9/6 = 3/2
AC/A'C' = 12/8 = 3/2
Por lo tanto, podemos concluir que los dos triángulos son semejantes y que los lados correspondientes están en una proporción de 3/2.
Teorema de Tales inverso
El segundo teorema de Tales, también conocido como el teorema de Tales inverso, establece que si tenemos tres puntos en una recta y una serie de rectas paralelas que cortan a esa recta, entonces los segmentos que se forman son proporcionales. Esto significa que si tenemos tres puntos A, B y C en una recta y una serie de rectas paralelas que cortan a esa recta en los puntos D, E y F, entonces:
AD/DE = AB/BC = AF/FC
Ejemplo:
Si tenemos una recta con tres puntos A, B y C, y una serie de rectas paralelas que cortan a esa recta en los puntos D, E y F, podemos usar el teorema de Tales inverso para encontrar la proporción entre los segmentos que se forman.
Si AD mide 3 unidades y DE mide 2 unidades, entonces:
AD/DE = 3/2
Si AB mide 6 unidades y BC mide 4 unidades, entonces:
AB/BC = 6/4 = 3/2
Si AF mide 9 unidades y FC mide 6 unidades, entonces:
AF/FC = 9/6 = 3/2
Por lo tanto, podemos concluir que los segmentos que se forman son proporcionales y que la proporción entre ellos es de 3/2.
Teorema de Tales generalizado
El tercer teorema de Tales, también conocido como el teorema de Tales generalizado, establece que si tenemos una serie de rectas paralelas que cortan a dos rectas transversales, entonces los segmentos que se forman son proporcionales. Esto significa que si tenemos dos rectas transversales AB y CD, y una serie de rectas paralelas que cortan a esas rectas transversales en los puntos E, F, G, H, I y J, entonces:
AE/EB = CF/FD = GH/HI = IJ/JD
Ejemplo:
Si tenemos dos rectas transversales AB y CD, y una serie de rectas paralelas que cortan a esas rectas transversales en los puntos E, F, G, H, I y J, podemos usar el teorema de Tales generalizado para encontrar la proporción entre los segmentos que se forman.
Si AE mide 2 unidades y EB mide 3 unidades, entonces:
AE/EB = 2/3
Si CF mide 4 unidades y FD mide 6 unidades, entonces:
CF/FD = 4/6 = 2/3
Si GH mide 8 unidades y HI mide 12 unidades, entonces:
GH/HI = 8/12 = 2/3
Si IJ mide 10 unidades y JD mide 15 unidades, entonces:
IJ/JD = 10/15 = 2/3
Por lo tanto, podemos concluir que los segmentos que se forman son proporcionales y que la proporción entre ellos es de 2/3.
Conclusión
Los teoremas de Tales son fundamentales en la geometría y se utilizan para resolver problemas de proporciones en triángulos y otras figuras geométricas. El primer teorema de Tales establece que si dos triángulos son semejantes, entonces las longitudes de los lados correspondientes son proporcionales. El segundo teorema de Tales, también conocido como el teorema de Tales inverso, establece que si tenemos tres puntos en una recta y una serie de rectas paralelas que cortan a esa recta, entonces los segmentos que se forman son proporcionales. El tercer teorema de Tales, también conocido como el teorema de Tales generalizado, establece que si tenemos una serie de rectas paralelas que cortan a dos rectas transversales, entonces los segmentos que se forman son proporcionales.
Preguntas frecuentes
¿Qué es la geometría?
La geometría es una rama de las matemáticas que se ocupa del estudio de las formas, tamaños, posiciones y dimensiones de los objetos en el espacio.
¿Quién fue Tales de Mileto?
Tales de Mileto fue un matemático, filósofo y científico griego que vivió en el siglo VI a.C. Es considerado uno de los siete sabios de Grecia y es conocido por sus contribuciones a la geometría y la astronomía.
¿Qué es un triángulo semejante?
Un triángulo semejante es un triángulo que tiene los mismos ángulos que otro triángulo, pero que puede tener un tamaño diferente.
¿Qué es una recta transversal?
Una recta transversal es una recta que intersecta a otras dos rectas en diferentes puntos.
¿Qué es una proporción?
Una proporción es una relación matemática entre dos o más cantidades que expresa cuántas veces una cantidad es mayor o menor que otra cantidad.
Deja una respuesta