Descubre las reglas fundamentales de álgebra booleana

El álgebra booleana es una rama de las matemáticas que se basa en el uso de operaciones lógicas para la manipulación de valores binarios (0 y 1). Esta rama es fundamental en el diseño de circuitos digitales y en la programación de sistemas informáticos. En este artículo, te presentaremos las reglas fundamentales de álgebra booleana que necesitas conocer para poder aplicarla de manera efectiva.

¿Qué es el álgebra booleana?

El álgebra booleana es una rama de las matemáticas que se centra en el estudio de operaciones lógicas aplicadas a valores binarios. En otras palabras, se trata de un conjunto de reglas que nos permiten manipular y transformar valores binarios (0 y 1) para obtener resultados lógicos.

Esta rama de las matemáticas es fundamental en el diseño de circuitos digitales y en la programación de sistemas informáticos. En el contexto de los circuitos digitales, el álgebra booleana se utiliza para diseñar circuitos lógicos que permiten realizar operaciones computacionales básicas.

Las reglas fundamentales de álgebra booleana

Existen varias reglas fundamentales de álgebra booleana que necesitas conocer para poder aplicarla de manera efectiva. Estas reglas se dividen en dos categorías: operaciones básicas y leyes de álgebra booleana.

Operaciones básicas

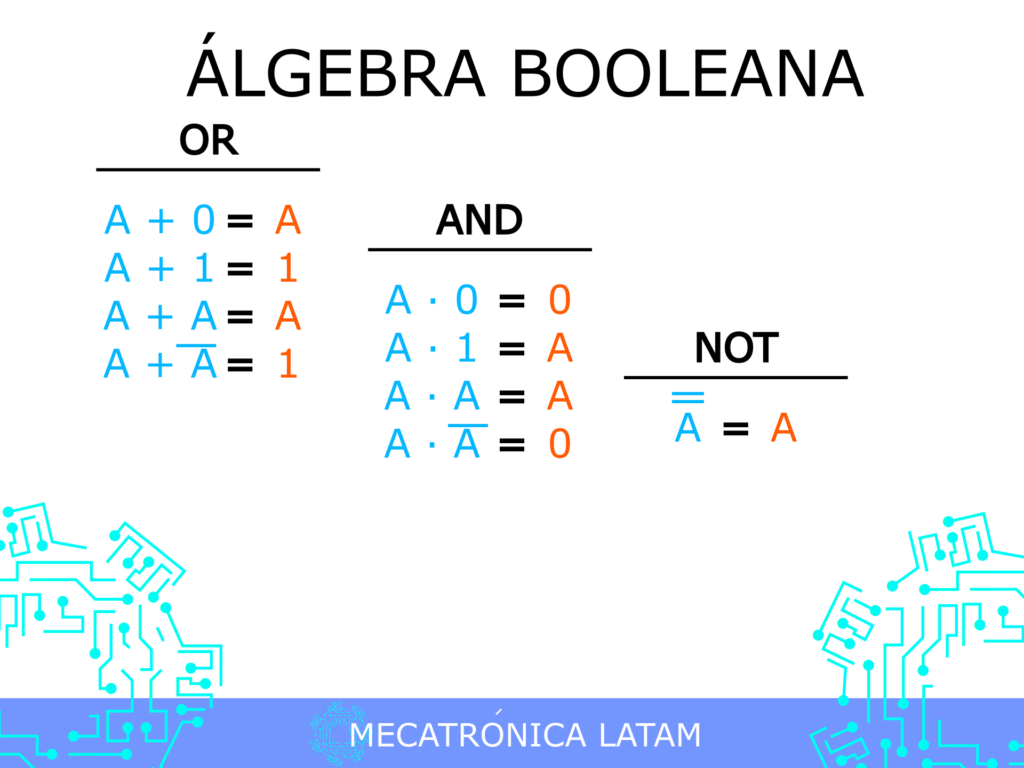
Las operaciones básicas del álgebra booleana son AND, OR y NOT. Veamos en qué consiste cada una de ellas:

• AND: se utiliza para determinar si dos valores binarios son iguales a 1. La operación AND se representa con el símbolo "&". Por ejemplo, si tenemos los valores binarios 1 y 0, la operación AND nos dará como resultado 0, ya que uno de los valores es 0.
• OR: se utiliza para determinar si al menos uno de los valores binarios es igual a 1. La operación OR se representa con el símbolo "|". Por ejemplo, si tenemos los valores binarios 1 y 0, la operación OR nos dará como resultado 1, ya que al menos uno de los valores es 1.
• NOT: se utiliza para invertir el valor de un bit. La operación NOT se representa con el símbolo "~". Por ejemplo, si tenemos el valor binario 1, la operación NOT nos dará como resultado 0.

Leyes de álgebra booleana

Las leyes de álgebra booleana son reglas que nos permiten simplificar expresiones booleanas y hacer más fácil su manipulación. Las leyes de álgebra booleana más importantes son las siguientes:

• Ley de la identidad: cualquier valor binario AND con 1 o OR con 0 es igual al valor binario original. Por ejemplo, 1 AND 1 = 1.
• Ley de la negación: cualquier valor binario AND con 0 o OR con 1 es igual al valor binario negado. Por ejemplo, 0 OR 1 = 1 (negado = 0).
• Ley de la conmutatividad: el orden en que se realizan las operaciones AND y OR no afecta el resultado final. Por ejemplo, 1 AND 0 es lo mismo que 0 AND 1.
• Ley de la asociatividad: el agrupamiento de los valores binarios en una expresión AND o OR no afecta al resultado final. Por ejemplo, (1 AND 0) AND 1 es lo mismo que 1 AND (0 AND 1).
• Ley de la distributividad: la operación AND distribuye sobre la operación OR y viceversa. Por ejemplo, 1 AND (0 OR 1) es lo mismo que (1 AND 0) OR (1 AND 1).
• Ley de la absorción: cualquier valor binario que se AND con 0 o se OR con 1 se convierte en 0 o 1, respectivamente. Por ejemplo, 1 AND 0 = 0.
• Ley de Morgan: la negación de una expresión AND o OR es igual a la operación OR o AND respectivamente, con los valores binarios negados. Por ejemplo, ~(1 AND 0) es lo mismo que (~1 OR ~0).

Conclusión

El álgebra booleana es una rama fundamental de las matemáticas que se utiliza en la programación de sistemas informáticos y el diseño de circuitos digitales. Las reglas fundamentales de álgebra booleana que hemos presentado en este artículo te permitirán manipular y transformar valores binarios de manera efectiva. Es importante conocer estas reglas para poder aplicarlas de manera adecuada en proyectos de programación y diseño de circuitos.

Preguntas frecuentes

1. ¿Qué es una expresión booleana?

Una expresión booleana es una combinación de valores binarios (0 y 1) y operaciones lógicas (AND, OR y NOT) que nos permite representar una proposición lógica.

2. ¿Para qué se utiliza el álgebra booleana?

El álgebra booleana se utiliza en el diseño de circuitos digitales y en la programación de sistemas informáticos para realizar operaciones lógicas y manipular valores binarios.

3. ¿Qué es la operación NOT en álgebra booleana?

La operación NOT en álgebra booleana se utiliza para invertir el valor de un bit. Por ejemplo, si tenemos el valor binario 1, la operación NOT nos dará como resultado 0.

4. ¿Qué son las leyes de álgebra booleana?

Las leyes de álgebra booleana son reglas que nos permiten simplificar expresiones booleanas y hacer más fácil su manipulación. Estas leyes incluyen la ley de la identidad, ley de la negación, ley de la conmutatividad, ley de la asociatividad, ley de la distributividad, ley de la absorción y ley de Morgan.

5. ¿Qué es la ley de Morgan en álgebra booleana?

La ley de Morgan en álgebra booleana establece que la negación de una expresión AND o OR es igual a la operación OR o AND respectivamente, con los valores binarios negados. Por ejemplo, ~(1 AND 0) es lo mismo que (~1 OR ~0).