Descubre las razones trigonométricas: seno, coseno y tangente

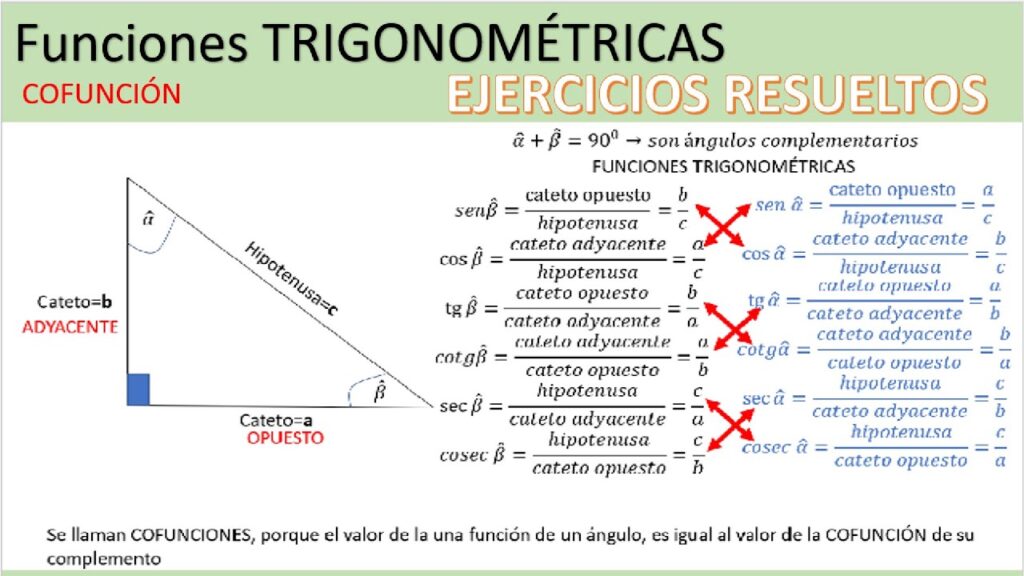
¿Alguna vez te has preguntado cómo se calculan las distancias entre dos puntos en un mapa, la altura de una montaña o la inclinación de un edificio? Todas estas medidas se pueden calcular utilizando las razones trigonométricas, específicamente el seno, coseno y tangente. En este artículo, descubrirás qué son estas razones, cómo se calculan y para qué se utilizan.

¿Qué son las razones trigonométricas?

Las razones trigonométricas son relaciones matemáticas entre los lados y ángulos de un triángulo rectángulo. Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90 grados. Los otros dos ángulos del triángulo son agudos, es decir, menores a 90 grados.

Las razones trigonométricas más comunes son el seno, coseno y tangente, pero también existen otras menos conocidas como la secante, cosecante y cotangente.

¿Qué es el seno?

El seno (sin) es una de las razones trigonométricas más utilizadas. Se define como la longitud del cateto opuesto al ángulo dividido por la longitud de la hipotenusa del triángulo rectángulo. En otras palabras, el seno de un ángulo es igual a la altura del triángulo que se encuentra frente a ese ángulo dividido por la distancia desde la base del triángulo hasta la hipotenusa. El seno se representa matemáticamente como:

sin θ = o / h

Donde θ es el ángulo, o es el cateto opuesto y h es la hipotenusa.

Ejemplo:

Si tenemos un triángulo rectángulo con un ángulo de 30 grados, un cateto opuesto de 5 cm y una hipotenusa de 10 cm, podemos calcular el seno de ese ángulo de la siguiente manera:

sin 30° = 5/10 = 0.5

¿Qué es el coseno?

El coseno (cos) es otra de las razones trigonométricas más utilizadas. Se define como la longitud del cateto adyacente al ángulo dividido por la longitud de la hipotenusa del triángulo rectángulo. En otras palabras, el coseno de un ángulo es igual a la distancia desde la base del triángulo hasta el ángulo dividido por la distancia desde la base hasta la hipotenusa. El coseno se representa matemáticamente como:

cos θ = a / h

Donde θ es el ángulo, a es el cateto adyacente y h es la hipotenusa.

Ejemplo:

Si tenemos un triángulo rectángulo con un ángulo de 60 grados, un cateto adyacente de 4 cm y una hipotenusa de 8 cm, podemos calcular el coseno de ese ángulo de la siguiente manera:

cos 60° = 4/8 = 0.5

¿Qué es la tangente?

La tangente (tan) es la tercera razón trigonométrica más utilizada. Se define como la longitud del cateto opuesto al ángulo dividido por la longitud del cateto adyacente al ángulo. En otras palabras, la tangente de un ángulo es igual a la altura del triángulo que se encuentra frente a ese ángulo dividido por la distancia desde la base del triángulo hasta el ángulo. La tangente se representa matemáticamente como:

tan θ = o / a

Donde θ es el ángulo, o es el cateto opuesto y a es el cateto adyacente.

Ejemplo:

Si tenemos un triángulo rectángulo con un ángulo de 45 grados, un cateto opuesto de 3 cm y un cateto adyacente de 3 cm, podemos calcular la tangente de ese ángulo de la siguiente manera:

tan 45° = 3/3 = 1

¿Para qué se utilizan las razones trigonométricas?

Las razones trigonométricas se utilizan en una gran cantidad de situaciones en las que es necesario calcular distancias, alturas o ángulos. Algunas aplicaciones comunes incluyen:

- Navegación: Los navegantes utilizan las razones trigonométricas para calcular la distancia entre dos puntos en un mapa o para determinar la altura de un faro.
- Arquitectura: Los arquitectos utilizan las razones trigonométricas para calcular la inclinación de un techo o para determinar la altura de un edificio.
- Geología: Los geólogos utilizan las razones trigonométricas para calcular la altura de una montaña o la profundidad de una cueva.
- Física: Los físicos utilizan las razones trigonométricas para calcular la velocidad de un objeto en movimiento o para determinar la fuerza gravitatoria entre dos cuerpos.

Conclusión

Las razones trigonométricas son herramientas matemáticas muy útiles que se utilizan en una gran cantidad de situaciones, desde la navegación hasta la física. El seno, coseno y tangente son las razones más utilizadas y se definen en términos de los lados y ángulos de un triángulo rectángulo. Esperamos que este artículo te haya ayudado a comprender mejor qué son las razones trigonométricas y cómo se utilizan.

Preguntas frecuentes

1. ¿Qué es un triángulo rectángulo?

Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90 grados. Los otros dos ángulos del triángulo son agudos, es decir, menores a 90 grados.

2. ¿Cuáles son las razones trigonométricas más utilizadas?

Las razones trigonométricas más utilizadas son el seno, coseno y tangente.

3. ¿Cómo se calcula el seno de un ángulo?

El seno de un ángulo se calcula dividiendo la longitud del cateto opuesto al ángulo por la longitud de la hipotenusa del triángulo rectángulo.

4. ¿Para qué se utilizan las razones trigonométricas?

Las razones trigonométricas se utilizan en una gran cantidad de situaciones en las que es necesario calcular distancias, alturas o ángulos.

5. ¿Qué es la tangente?

La tangente es una de las razones trigonométricas más utilizadas y se define como la longitud del cateto opuesto al ángulo dividido por la longitud del cateto adyacente al ángulo.