Descubre las razones trigonométricas en triángulos rectángulos

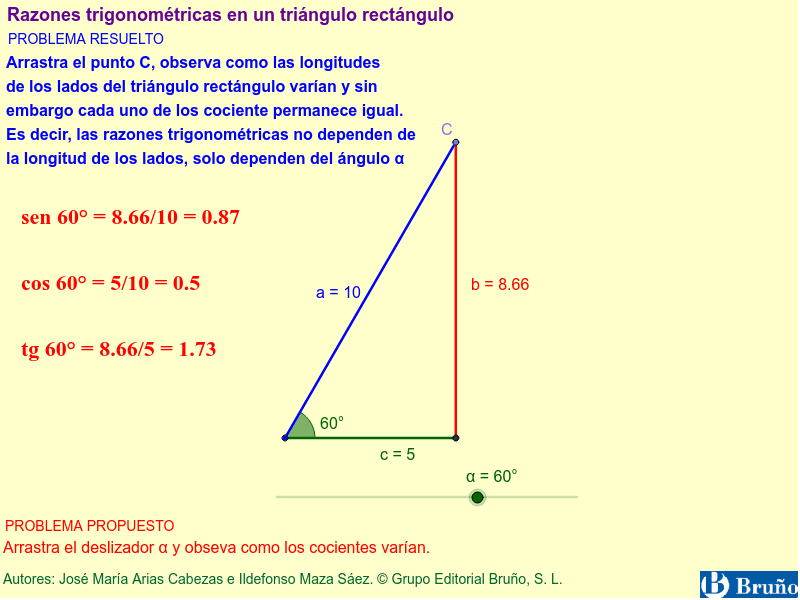
Si alguna vez has estudiado geometría, seguramente has oído hablar de los triángulos rectángulos. Estos son triángulos que tienen un ángulo recto, es decir, un ángulo de 90 grados. Los triángulos rectángulos son muy importantes en matemáticas y en la vida cotidiana, y una de las razones por las que son tan interesantes es porque se pueden utilizar para demostrar las razones trigonométricas.

Las razones trigonométricas son relaciones matemáticas entre los lados de un triángulo rectángulo y sus ángulos. Hay tres razones trigonométricas principales: el seno, el coseno y la tangente. Estas razones son muy útiles para resolver problemas trigonométricos, como calcular la altura de un edificio o la distancia entre dos puntos en un plano.

Las razones trigonométricas básicas

Antes de adentrarnos en las razones trigonométricas en triángulos rectángulos, es importante entender las razones básicas. Estas razones se basan en el círculo trigonométrico, que es un círculo en el que se han marcado los ángulos en grados o radianes. El círculo se divide en cuatro cuadrantes, y cada cuadrante representa un ángulo diferente.

La razón trigonométrica más básica es el seno. El seno de un ángulo se define como la longitud del cateto opuesto dividida por la longitud de la hipotenusa. En otras palabras, si tienes un triángulo rectángulo y quieres calcular el seno de uno de sus ángulos, debes dividir la longitud del cateto opuesto por la longitud de la hipotenusa.

La siguiente razón trigonométrica básica es el coseno. El coseno de un ángulo se define como la longitud del cateto adyacente dividida por la longitud de la hipotenusa. En otras palabras, si tienes un triángulo rectángulo y quieres calcular el coseno de uno de sus ángulos, debes dividir la longitud del cateto adyacente por la longitud de la hipotenusa.

La tercera razón trigonométrica básica es la tangente. La tangente de un ángulo se define como la longitud del cateto opuesto dividida por la longitud del cateto adyacente. En otras palabras, si tienes un triángulo rectángulo y quieres calcular la tangente de uno de sus ángulos, debes dividir la longitud del cateto opuesto por la longitud del cateto adyacente.

Razonamiento trigonométrico en triángulos rectángulos

Ahora que hemos repasado las razones trigonométricas básicas, podemos adentrarnos en el razonamiento trigonométrico en triángulos rectángulos. Como mencionamos anteriormente, en un triángulo rectángulo, la hipotenusa es el lado más largo y está opuesto al ángulo recto. Los otros dos lados del triángulo se llaman catetos.

Si tenemos un triángulo rectángulo con un ángulo agudo y conocemos la longitud de uno de los catetos y la hipotenusa, podemos utilizar el teorema de Pitágoras para calcular la longitud del otro cateto. Una vez que conocemos la longitud de los catetos y la hipotenusa, podemos utilizar las razones trigonométricas para calcular los ángulos y las longitudes de los otros lados del triángulo.

Cálculo del seno, coseno y tangente en triángulos rectángulos

Para calcular el seno, el coseno y la tangente de un ángulo en un triángulo rectángulo, debemos conocer las longitudes de los lados del triángulo. Supongamos que tenemos un triángulo rectángulo con un ángulo agudo θ, un cateto adyacente a θ de longitud a, un cateto opuesto a θ de longitud b y una hipotenusa de longitud c.

Para calcular el seno de θ, debemos dividir la longitud del cateto opuesto por la longitud de la hipotenusa:

sen(θ) = b/c

Para calcular el coseno de θ, debemos dividir la longitud del cateto adyacente por la longitud de la hipotenusa:

cos(θ) = a/c

Para calcular la tangente de θ, debemos dividir la longitud del cateto opuesto por la longitud del cateto adyacente:

tan(θ) = b/a

Usos de las razones trigonométricas en la vida cotidiana

Las razones trigonométricas se utilizan en muchos campos, como la ingeniería, la arquitectura, la navegación y la física. Pero también tienen aplicaciones prácticas en la vida cotidiana. Por ejemplo, si quieres medir la altura de un árbol o de un edificio, puedes utilizar la razón tangente para calcular la altura. Si sabes la distancia a la que estás del árbol o del edificio, y el ángulo que forma tu línea de visión con la parte superior del objeto, puedes utilizar la razón tangente para calcular la altura.

Otro ejemplo de aplicación de las razones trigonométricas en la vida cotidiana es en la construcción de rampas. Si estás construyendo una rampa para sillas de ruedas o para bicicletas, debes asegurarte de que la inclinación de la rampa sea segura y cómoda para las personas que la utilizarán. Puedes utilizar la razón seno para calcular la inclinación de la rampa y asegurarte de que no es demasiado empinada.

Conclusión

Las razones trigonométricas en triángulos rectángulos son muy útiles para resolver problemas matemáticos y para aplicaciones prácticas en la vida cotidiana. El seno, el coseno y la tangente son las razones trigonométricas principales y se basan en las longitudes de los lados de un triángulo rectángulo y los ángulos opuestos. Conociendo estas razones, podemos calcular los ángulos y las longitudes de los lados de un triángulo rectángulo y resolver problemas trigonométricos.

Preguntas frecuentes

¿Qué es un triángulo rectángulo?

Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir, un ángulo de 90 grados.

¿Qué son las razones trigonométricas?

Las razones trigonométricas son relaciones matemáticas entre los lados de un triángulo rectángulo y sus ángulos. Las razones trigonométricas principales son el seno, el coseno y la tangente.

¿Cómo se calculan las razones trigonométricas en un triángulo rectángulo?

Para calcular el seno de un ángulo en un triángulo rectángulo, debes dividir la longitud del cateto opuesto por la