Descubre las propiedades de la lógica proposicional
La lógica proposicional es una herramienta fundamental para la resolución de problemas y la toma de decisiones en diversos ámbitos, desde la informática hasta la filosofía. Esta rama de la lógica se enfoca en el estudio de las proposiciones, es decir, enunciados que pueden ser verdaderos o falsos. En este artículo, te invitamos a descubrir algunas de las propiedades más importantes de la lógica proposicional.
- 1. Las proposiciones se pueden combinar
- 2. La lógica proposicional se puede representar mediante tablas de verdad
- 3. La lógica proposicional permite la simplificación de expresiones
- 4. La lógica proposicional se puede aplicar a la programación
- 5. La lógica proposicional tiene aplicaciones en la filosofía y la teoría de la argumentación
- Conclusión
-
Preguntas frecuentes
- 1. ¿Qué es una proposición en lógica proposicional?
- 2. ¿Qué son los conectores lógicos en lógica proposicional?
- 3. ¿Por qué es importante la lógica proposicional en programación?
- 4. ¿Cómo se puede simplificar una expresión en lógica proposicional?
- 5. ¿Qué aplicaciones tiene la lógica proposicional en la filosofía?
1. Las proposiciones se pueden combinar
Una de las características más importantes de la lógica proposicional es que las proposiciones se pueden combinar para formar nuevas proposiciones. Esto se logra mediante el uso de los llamados conectores lógicos, como la conjunción (y), la disyunción (o) y la negación (no). Por ejemplo, si A es una proposición verdadera y B es una proposición falsa, la proposición "A y B" es falsa, mientras que la proposición "A o B" es verdadera.
2. La lógica proposicional se puede representar mediante tablas de verdad
Una tabla de verdad es una herramienta que se utiliza para representar las diferentes combinaciones de verdad y falsedad de las proposiciones. En una tabla de verdad, se enumeran todas las posibles combinaciones de verdad y falsedad de las proposiciones individuales, y se determina el valor de verdad de la proposición compuesta para cada combinación. De esta manera, es posible verificar si una proposición compuesta es verdadera o falsa.
3. La lógica proposicional permite la simplificación de expresiones
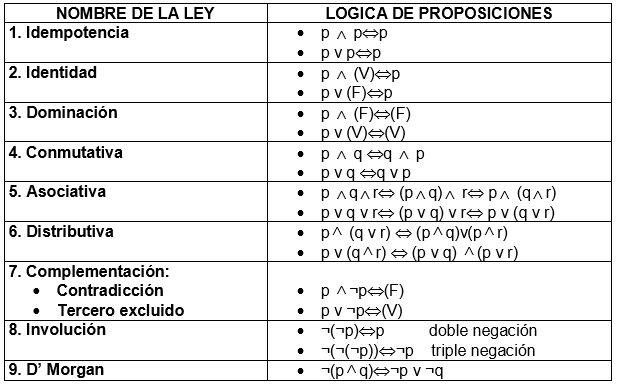
Una de las ventajas de la lógica proposicional es que permite la simplificación de expresiones complejas mediante el uso de las reglas de equivalencia lógica. Estas reglas establecen que dos proposiciones son equivalentes si tienen el mismo valor de verdad para todas las combinaciones de verdad y falsedad de las proposiciones individuales. De esta manera, es posible reducir una expresión compleja a una más simple y fácil de entender.
4. La lógica proposicional se puede aplicar a la programación
La lógica proposicional es una herramienta fundamental en el diseño de algoritmos y programas informáticos. Los programadores utilizan los conectores lógicos para establecer condiciones y tomar decisiones en el código fuente. Por ejemplo, si se desea que un programa realice una acción sólo si se cumplen dos condiciones, se puede utilizar el conector lógico "y" para combinar ambas condiciones en una sola instrucción.
5. La lógica proposicional tiene aplicaciones en la filosofía y la teoría de la argumentación
La lógica proposicional también es de gran importancia en la filosofía y la teoría de la argumentación. La capacidad de evaluar la verdad o falsedad de las proposiciones y las expresiones complejas es esencial para el razonamiento lógico y la construcción de argumentos sólidos. Además, la lógica proposicional permite identificar falacias y errores en la argumentación.
Conclusión
La lógica proposicional es una herramienta fundamental en diversos ámbitos, desde la informática hasta la filosofía. Las propiedades que hemos descubierto en este artículo demuestran la importancia de las proposiciones, los conectores lógicos y las tablas de verdad en la lógica proposicional. Además, hemos visto cómo esta rama de la lógica se puede aplicar a la programación y la teoría de la argumentación, lo que demuestra su versatilidad y utilidad.
Preguntas frecuentes
1. ¿Qué es una proposición en lógica proposicional?
Una proposición es un enunciado que puede ser verdadero o falso. Por ejemplo, "el cielo es azul" es una proposición que es verdadera, mientras que "el sol es una estrella" es una proposición que es falsa.
2. ¿Qué son los conectores lógicos en lógica proposicional?
Los conectores lógicos son términos que se utilizan para combinar proposiciones y formar nuevas proposiciones. Los principales conectores lógicos son la conjunción (y), la disyunción (o) y la negación (no).
3. ¿Por qué es importante la lógica proposicional en programación?
La lógica proposicional es esencial en programación porque permite establecer condiciones y tomar decisiones en el código fuente. Los programadores utilizan los conectores lógicos para construir algoritmos y programas informáticos.
4. ¿Cómo se puede simplificar una expresión en lógica proposicional?
Se pueden simplificar expresiones complejas en lógica proposicional mediante el uso de las reglas de equivalencia lógica. Estas reglas establecen que dos proposiciones son equivalentes si tienen el mismo valor de verdad para todas las combinaciones de verdad y falsedad de las proposiciones individuales.
5. ¿Qué aplicaciones tiene la lógica proposicional en la filosofía?
La lógica proposicional es de gran importancia en la filosofía porque permite evaluar la verdad o falsedad de las proposiciones y las expresiones complejas, lo que es esencial para el razonamiento lógico y la construcción de argumentos sólidos. Además, permite identificar falacias y errores en la argumentación.
Deja una respuesta