Descubre las leyes fundamentales de Álgebra Booleana

Si alguna vez has trabajado con circuitos electrónicos, es muy probable que hayas oído hablar de Álgebra Booleana. Esta rama de la matemática se utiliza para simplificar expresiones lógicas y diseñar circuitos digitales. En este artículo, te presentaré las leyes fundamentales de Álgebra Booleana que te ayudarán a entender cómo funciona esta herramienta.

¿Qué es Álgebra Booleana?

Álgebra Booleana es una rama de la matemática que se centra en el estudio de las operaciones lógicas y las relaciones entre los valores verdadero y falso. Fue desarrollada por George Boole en el siglo XIX y se utiliza para simplificar expresiones lógicas y diseñar circuitos digitales.

Las leyes fundamentales de Álgebra Booleana

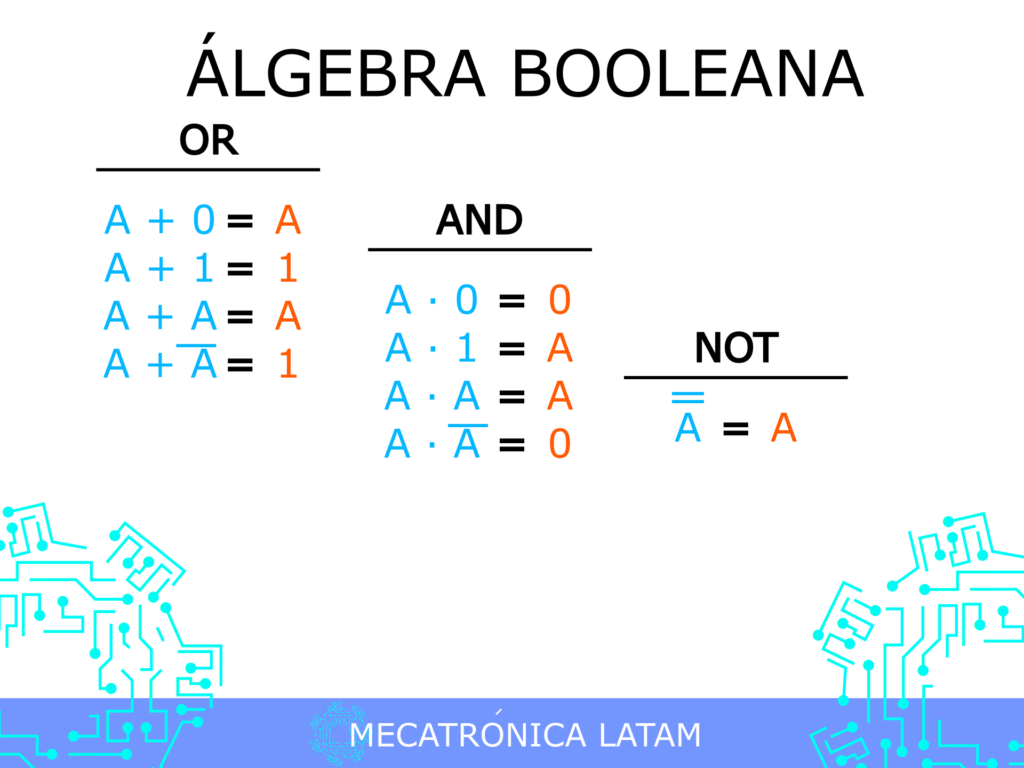
Estas son las leyes fundamentales de Álgebra Booleana que te ayudarán a simplificar expresiones lógicas y diseñas circuitos digitales.

Ley de la Identidad

La ley de la identidad establece que si se suma cero o se multiplica por uno cualquier valor, el resultado será el mismo valor. En términos de Álgebra Booleana, la ley de la identidad se expresa así:

A + 0 = A

A * 1 = A

Ley de la Complementación

La ley de la complementación establece que el complemento de un valor es igual a su negación. En términos de Álgebra Booleana, la ley de la complementación se expresa así:

A + A' = 1

A * A' = 0

Ley de la Commutación

La ley de la commutación establece que el orden de los valores no afecta al resultado de la operación. En términos de Álgebra Booleana, la ley de la commutación se expresa así:

A + B = B + A

A * B = B * A

Ley de la Asociación

La ley de la asociación establece que el agrupamiento de los valores no afecta al resultado de la operación. En términos de Álgebra Booleana, la ley de la asociación se expresa así:

(A + B) + C = A + (B + C)

(A * B) * C = A * (B * C)

Ley de la Distribución

La ley de la distribución establece que la multiplicación se distribuye sobre la suma y viceversa. En términos de Álgebra Booleana, la ley de la distribución se expresa así:

A * (B + C) = A * B + A * C

A + (B * C) = (A + B) * (A + C)

Ley de la Absorción

La ley de la absorción establece que si uno de los valores es cero, el resultado será cero. En términos de Álgebra Booleana, la ley de la absorción se expresa así:

A + (A * B) = A

A * (A + B) = A

Ley de De Morgan

La ley de De Morgan establece que la negación de una suma o una multiplicación es igual a la suma o la multiplicación de las negaciones de los valores. En términos de Álgebra Booleana, la ley de De Morgan se expresa así:

(A + B)' = A' * B'

(A * B)' = A' + B'

Conclusión

Álgebra Booleana es una herramienta muy útil para simplificar expresiones lógicas y diseñar circuitos digitales. Las leyes fundamentales de Álgebra Booleana te ayudarán a entender cómo funciona esta herramienta y cómo simplificar expresiones lógicas.

Preguntas frecuentes

¿Cuál es la diferencia entre Álgebra Booleana y Álgebra convencional?

Álgebra Booleana se centra en el estudio de las operaciones lógicas y las relaciones entre los valores verdadero y falso, mientras que Álgebra convencional se centra en las operaciones aritméticas y las relaciones entre los números.

¿Cómo se utiliza Álgebra Booleana en los circuitos electrónicos?

Álgebra Booleana se utiliza para diseñar circuitos digitales y simplificar expresiones lógicas. Los circuitos electrónicos se basan en las operaciones lógicas y las relaciones entre los valores verdadero y falso.

¿Por qué es importante Álgebra Booleana?

Álgebra Booleana es importante porque nos permite simplificar expresiones lógicas y diseñar circuitos digitales de manera más eficiente. También es una herramienta fundamental en la teoría de la información y la computación.

¿Cómo puedo aprender más sobre Álgebra Booleana?

Puedes aprender más sobre Álgebra Booleana a través de libros y cursos especializados en matemáticas y electrónica. También hay muchos recursos en línea, como tutoriales y videos, que pueden ayudarte a comprender mejor esta herramienta.

¿Dónde se utiliza Álgebra Booleana además de los circuitos electrónicos?

Álgebra Booleana se utiliza en la teoría de la información, la computación, la inteligencia artificial y la lógica matemática. También se utiliza en la teoría de conjuntos y la teoría de la probabilidad.