Descubre las identidades trigonométricas de forma lógica

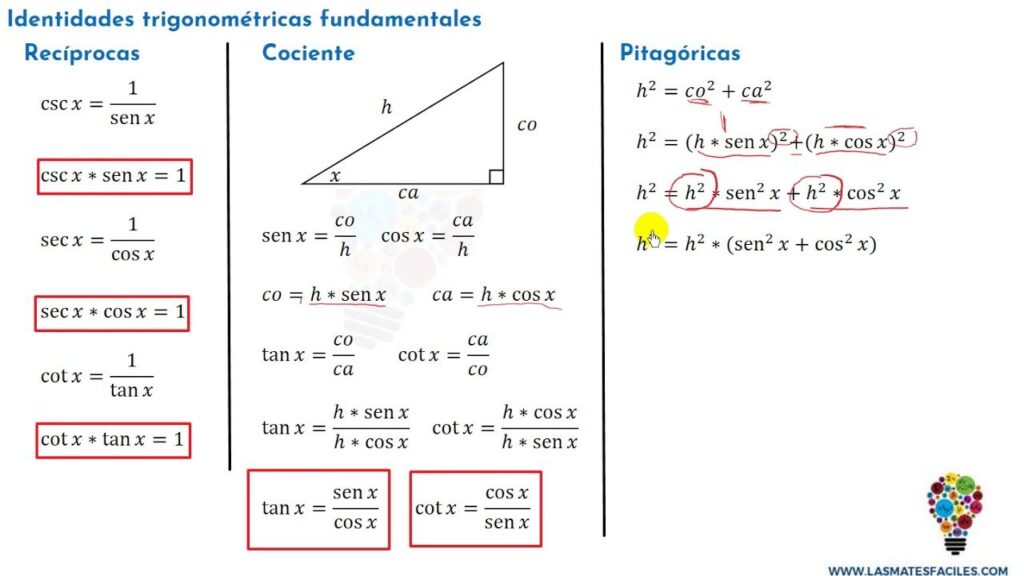
La trigonometría es una rama de las matemáticas que se encarga del estudio de las relaciones entre los lados y los ángulos de un triángulo. Las identidades trigonométricas son igualdades matemáticas que relacionan las funciones trigonométricas de un ángulo con las funciones trigonométricas de otro ángulo o con las constantes matemáticas como el número pi.

En este artículo, descubrirás cómo obtener las identidades trigonométricas de forma lógica, utilizando conceptos básicos de geometría y algebra. Además, te enseñaremos algunas estrategias para recordarlas fácilmente.

¿Qué son las identidades trigonométricas?

Las identidades trigonométricas son ecuaciones que relacionan las funciones trigonométricas de un ángulo con las funciones trigonométricas de otro ángulo o con las constantes matemáticas como el número pi. Estas ecuaciones son verdaderas para cualquier valor de los ángulos involucrados.

Identidades trigonométricas básicas

Las identidades trigonométricas básicas son las siguientes:

- Seno: sen(a + b) = sen(a)cos(b) + cos(a)sen(b)
- Coseno: cos(a + b) = cos(a)cos(b) - sen(a)sen(b)
- Tangente: tan(a + b) = (tan(a) + tan(b)) / (1 - tan(a)tan(b))
- Cotangente: cot(a + b) = (cot(a)cot(b) - 1) / (cot(b) + cot(a))

Estas identidades se pueden demostrar utilizando la definición de las funciones trigonométricas y las propiedades de las funciones trigonométricas de ángulos complementarios.

Identidades trigonométricas adicionales

Además de las identidades trigonométricas básicas, existen otras identidades trigonométricas que se pueden obtener a partir de ellas:

- Identidades de ángulos dobles: sen(2a) = 2sen(a)cos(a), cos(2a) = cos²(a) - sen²(a), tan(2a) = (2tan(a)) / (1 - tan²(a))
- Identidades de ángulos mitad: sen(a/2) = ±√[(1 - cos(a)) / 2], cos(a/2) = ±√[(1 + cos(a)) / 2], tan(a/2) = ±√[(1 - cos(a)) / (1 + cos(a))]
- Identidades de ángulos complementarios: sen(π/2 - a) = cos(a), cos(π/2 - a) = sen(a), tan(π/2 - a) = 1 / tan(a)
- Identidades de ángulos suplementarios: sen(π - a) = sen(a), cos(π - a) = -cos(a), tan(π - a) = -tan(a)

Cómo recordar las identidades trigonométricas

Para recordar las identidades trigonométricas, es importante entender la lógica detrás de ellas. Por ejemplo, las identidades de ángulos dobles se pueden obtener a partir de la fórmula de la suma de ángulos (sen(a + b) y cos(a + b)), mientras que las identidades de ángulos mitad se pueden obtener a partir de las fórmulas de la mitad de ángulos (sen(a/2), cos(a/2) y tan(a/2)).

Además, es útil memorizar algunas identidades trigonométricas básicas, como el seno y coseno de ángulos especiales (0°, 30°, 45°, 60°, 90°) y las relaciones entre las funciones trigonométricas (seno y coseno, tangente y cotangente).

Conclusión

Las identidades trigonométricas son ecuaciones que relacionan las funciones trigonométricas de un ángulo con las funciones trigonométricas de otro ángulo o con las constantes matemáticas como el número pi. Estas ecuaciones son verdaderas para cualquier valor de los ángulos involucrados. Las identidades trigonométricas se pueden obtener utilizando conceptos básicos de geometría y algebra, y es importante entender la lógica detrás de ellas para recordarlas fácilmente.

Preguntas frecuentes

1. ¿Por qué son importantes las identidades trigonométricas?

Las identidades trigonométricas son importantes porque se utilizan en muchos campos de la ciencia y la ingeniería, como la física, la estadística, la acústica y la electrónica. Además, son útiles para simplificar expresiones matemáticas y resolver ecuaciones trigonométricas.

2. ¿Cómo se pueden aplicar las identidades trigonométricas en la vida cotidiana?

Las identidades trigonométricas se pueden aplicar en la vida cotidiana en situaciones que involucran medición de ángulos y distancias, como la construcción de edificios y puentes, la navegación marítima y aérea, y la astronomía.

3. ¿Cuál es la diferencia entre una función trigonométrica y una identidad trigonométrica?

Una función trigonométrica es una función matemática que relaciona un ángulo con una proporción de los lados de un triángulo rectángulo. Una identidad trigonométrica es una ecuación que relaciona las funciones trigonométricas de un ángulo con las funciones trigonométricas de otro ángulo o con las constantes matemáticas como el número pi.

4. ¿Por qué se llaman identidades trigonométricas?

Las identidades trigonométricas se llaman así porque son igualdades matemáticas que son verdaderas para cualquier valor de los ángulos involucrados, es decir, identidades matemáticas.

5. ¿Cómo se pueden demostrar las identidades trigonométricas?

Las identidades trigonométricas se pueden demostrar utilizando la definición de las funciones trigonométricas y las propiedades de las funciones trigonométricas de ángulos complementarios. También se pueden demostrar utilizando las fórmulas de la suma y diferencia de ángulos, y las fórmulas de la mitad de ángulos.