Descubre las características únicas de la lógica intuicionista

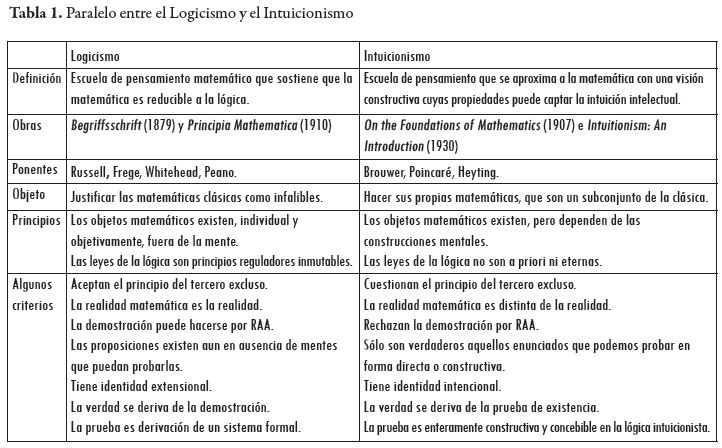
La lógica intuicionista es una corriente filosófica y matemática que se enfoca en la intuición y la construcción de conceptos a partir de la experiencia. A diferencia de otras corrientes lógicas, la intuicionista no acepta el principio de tercero excluido, que establece que algo es verdadero o falso. En este artículo, descubrirás las características únicas de la lógica intuicionista, su aplicación en la matemática y su relación con la filosofía.

1. Principio de tercero excluido

La lógica intuicionista rechaza el principio de tercero excluido, que establece que algo es verdadero o falso, sin posibilidad de una tercera opción. En cambio, la lógica intuicionista acepta que hay proposiciones que no pueden ser afirmadas o negadas, sino que requieren más información o contexto para ser resueltas.

Por ejemplo, en la lógica clásica, se puede afirmar que una proposición es verdadera o falsa, pero en la lógica intuicionista, una proposición podría ser verdadera, falsa, o no tener un valor de verdad definido.

2. Construcción de conceptos

La lógica intuicionista se enfoca en la construcción de conceptos a partir de la experiencia y la intuición. En lugar de partir de premisas universales, la lógica intuicionista busca construir conceptos a partir de la experiencia y la observación.

Por ejemplo, en la lógica clásica, se parte de premisas universales, como "todos los hombres son mortales". En cambio, en la lógica intuicionista, se puede partir de la observación de que un hombre en particular es mortal, y a partir de ahí, construir el concepto de mortalidad.

3. Lógica constructiva

La lógica intuicionista se considera una lógica constructiva, ya que se enfoca en la construcción de conceptos a partir de la experiencia y la intuición. En lugar de partir de premisas universales, la lógica intuicionista busca construir conceptos a partir de la experiencia y la observación.

Por ejemplo, en la lógica clásica, se puede afirmar que existe un número infinito de números primos, pero en la lógica intuicionista, se requiere construir un número primo a partir de la experiencia y la observación.

4. Matemática intuicionista

La lógica intuicionista se aplica en la matemática intuicionista, que es una rama de las matemáticas que se enfoca en la construcción de conceptos a partir de la experiencia y la intuición.

En la matemática intuicionista, se parte de la observación y la experiencia para construir conceptos matemáticos. Por ejemplo, en lugar de partir de la definición de un número natural como un conjunto infinito, se parte de la observación de que un número natural es un objeto matemático que se puede construir a partir de la sucesión de números anteriores.

5. Filosofía intuicionista

La lógica intuicionista también se relaciona con la filosofía, ya que se enfoca en la construcción de conceptos a partir de la experiencia y la intuición. En la filosofía intuicionista, se parte de la observación y la experiencia para construir conceptos filosóficos.

Por ejemplo, en lugar de partir de una definición universal de la verdad, se parte de la observación de que la verdad es un concepto que se construye a partir de la experiencia y la intuición.

Conclusión

La lógica intuicionista es una corriente filosófica y matemática que se enfoca en la intuición y la construcción de conceptos a partir de la experiencia. A diferencia de otras corrientes lógicas, la intuicionista no acepta el principio de tercero excluido, que establece que algo es verdadero o falso. La lógica intuicionista se considera una lógica constructiva, ya que se enfoca en la construcción de conceptos a partir de la experiencia y la intuición. En la matemática intuicionista, se parte de la observación y la experiencia para construir conceptos matemáticos. En la filosofía intuicionista, se parte de la observación y la experiencia para construir conceptos filosóficos.

Preguntas frecuentes

1. ¿Por qué la lógica intuicionista rechaza el principio de tercero excluido?

La lógica intuicionista rechaza el principio de tercero excluido porque considera que hay proposiciones que no pueden ser afirmadas o negadas, sino que requieren más información o contexto para ser resueltas.

2. ¿Cómo se aplica la lógica intuicionista en la matemática?

La lógica intuicionista se aplica en la matemática intuicionista, que se enfoca en la construcción de conceptos a partir de la experiencia y la intuición. En la matemática intuicionista, se parte de la observación y la experiencia para construir conceptos matemáticos.

3. ¿Qué es la filosofía intuicionista?

La filosofía intuicionista se enfoca en la construcción de conceptos filosóficos a partir de la experiencia y la intuición. En la filosofía intuicionista, se parte de la observación y la experiencia para construir conceptos filosóficos.

4. ¿Cuál es la diferencia entre la lógica clásica y la lógica intuicionista?

La lógica clásica parte de premisas universales, mientras que la lógica intuicionista se enfoca en la construcción de conceptos a partir de la experiencia y la intuición. La lógica intuicionista también rechaza el principio de tercero excluido, que establece que algo es verdadero o falso, sin posibilidad de una tercera opción.

5. ¿Qué es la lógica constructiva?

La lógica constructiva se refiere a la construcción de conceptos a partir de la experiencia y la intuición. La lógica intuicionista se considera una lógica constructiva, ya que se enfoca en la construcción de conceptos a partir de la experiencia y la intuición.