Descubre las 4 operaciones básicas con conjuntos
Los conjuntos son una herramienta matemática fundamental que se utiliza para categorizar objetos y conceptos en grupos. En la teoría de conjuntos, existen cuatro operaciones básicas que se pueden realizar entre conjuntos: la unión, la intersección, la diferencia y el complemento. En este artículo, vamos a abordar cada una de estas operaciones y explicar cómo funcionan.
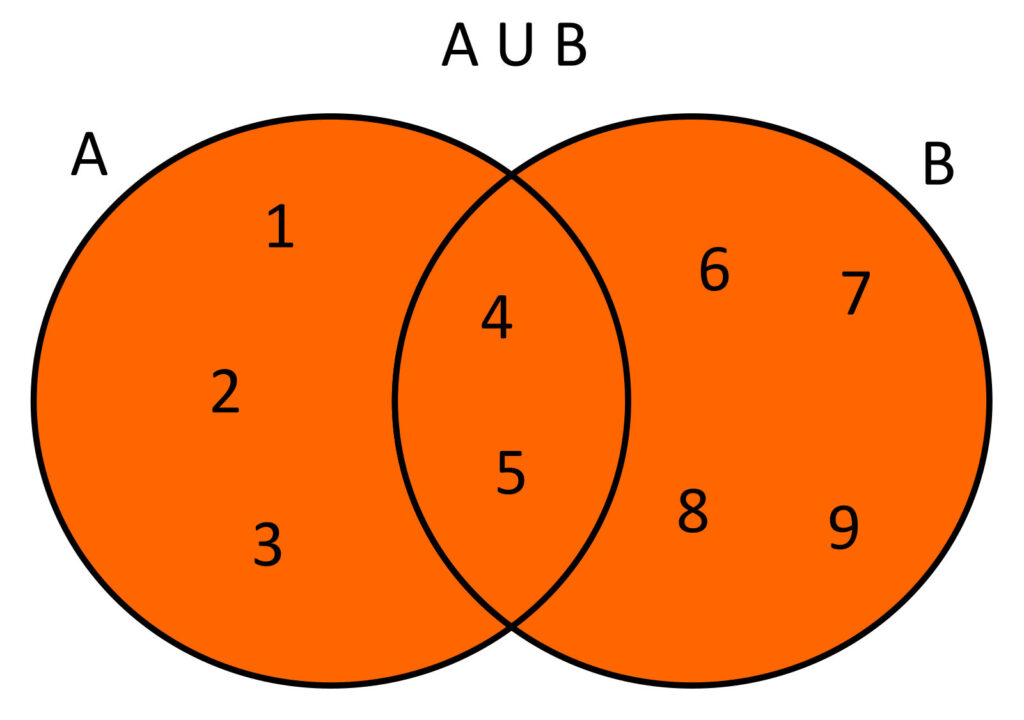
Unión
La unión es la operación que se utiliza para combinar dos conjuntos en uno solo. El resultado de la unión de dos conjuntos es un nuevo conjunto que contiene todos los elementos que pertenecen a cualquiera de los conjuntos originales. Por ejemplo, si tenemos el conjunto A = {1, 2, 3} y el conjunto B = {2, 4, 6}, la unión de ambos conjuntos sería A ∪ B = {1, 2, 3, 4, 6}.
Ejemplo:
A = {1, 2, 3}
B = {2, 4, 6}
A ∪ B = {1, 2, 3, 4, 6}
Intersección
La intersección es la operación que se utiliza para encontrar los elementos comunes entre dos conjuntos. El resultado de la intersección de dos conjuntos es un nuevo conjunto que contiene solo los elementos que pertenecen a ambos conjuntos originales. Por ejemplo, si tenemos el conjunto A = {1, 2, 3} y el conjunto B = {2, 4, 6}, la intersección de ambos conjuntos sería A ∩ B = {2}.
Ejemplo:
A = {1, 2, 3}
B = {2, 4, 6}
A ∩ B = {2}
Diferencia
La diferencia es la operación que se utiliza para encontrar los elementos que pertenecen a un conjunto pero no al otro. El resultado de la diferencia de dos conjuntos es un nuevo conjunto que contiene solo los elementos que pertenecen al primer conjunto pero no al segundo. Por ejemplo, si tenemos el conjunto A = {1, 2, 3} y el conjunto B = {2, 4, 6}, la diferencia de A con respecto a B sería A - B = {1, 3}.
Ejemplo:
A = {1, 2, 3}
B = {2, 4, 6}
A - B = {1, 3}
Complemento
El complemento es la operación que se utiliza para encontrar los elementos que no pertenecen a un conjunto dado. El resultado del complemento de un conjunto es un nuevo conjunto que contiene todos los elementos que no pertenecen al conjunto original en un conjunto universal dado. Por ejemplo, si tenemos el conjunto A = {1, 2, 3} y el conjunto universal U = {1, 2, 3, 4, 5, 6}, el complemento de A en U sería A' = {4, 5, 6}.
Ejemplo:
A = {1, 2, 3}
U = {1, 2, 3, 4, 5, 6}
A' = {4, 5, 6}
Conclusión
Las cuatro operaciones básicas con conjuntos son fundamentales en la teoría de conjuntos. Son herramientas matemáticas útiles para categorizar y clasificar objetos y conceptos. La unión combina dos conjuntos en uno solo, la intersección encuentra los elementos comunes entre dos conjuntos, la diferencia encuentra los elementos que pertenecen a un conjunto pero no al otro y el complemento encuentra los elementos que no pertenecen a un conjunto dado. Estas operaciones son la base para muchas otras operaciones y teoremas en la teoría de conjuntos.
Preguntas frecuentes
1. ¿Pueden aplicarse estas operaciones a conjuntos infinitos?
Sí, estas operaciones pueden aplicarse a conjuntos infinitos, siempre y cuando los conjuntos sean bien definidos.
2. ¿Pueden aplicarse estas operaciones a conjuntos vacíos?
Sí, estas operaciones pueden aplicarse a conjuntos vacíos, aunque los resultados pueden variar dependiendo de la operación.
3. ¿Pueden combinarse dos operaciones básicas en una sola expresión?
Sí, es posible combinar dos operaciones básicas en una sola expresión, como por ejemplo (A ∪ B) - (C ∩ D).
4. ¿Pueden estas operaciones utilizarse en álgebra?
Sí, estas operaciones pueden utilizarse en álgebra y en otras ramas de las matemáticas.
5. ¿Qué otros teoremas y operaciones se basan en estas cuatro operaciones básicas?
Estas operaciones son la base para muchos otros teoremas y operaciones en la teoría de conjuntos, como las leyes de De Morgan, la ley distributiva, la ley asociativa, entre otras.
Deja una respuesta