Descubre las 4 fórmulas del Teorema de Pitágoras

Si estás estudiando geometría, seguro has escuchado hablar del famoso Teorema de Pitágoras. Este teorema es una de las herramientas más importantes en matemáticas, y se utiliza para calcular la longitud de los lados de un triángulo rectángulo. Pero, ¿sabías que existen diferentes fórmulas para aplicar este teorema? En este artículo, descubrirás las 4 fórmulas del Teorema de Pitágoras.

¿Qué es el Teorema de Pitágoras?

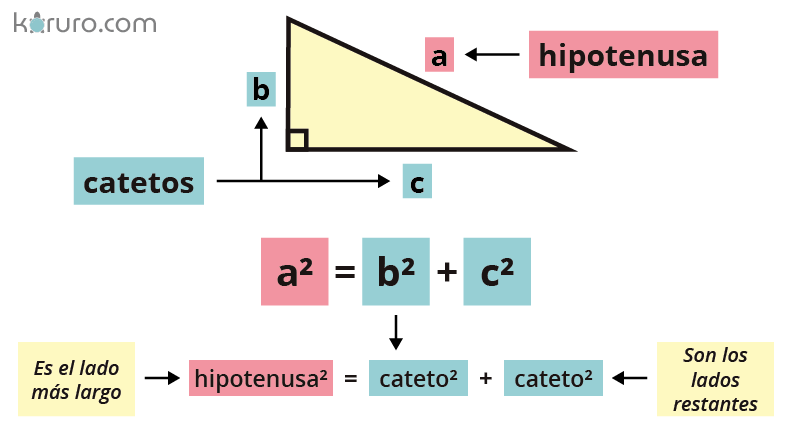
Antes de entrar en detalle sobre las fórmulas del teorema de Pitágoras, es importante saber en qué consiste. El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados.

En otras palabras, si llamamos "a" y "b" a los dos catetos (los lados que forman el ángulo recto) y "c" a la hipotenusa, entonces:

c² = a² + b²

Esta fórmula es muy útil para calcular la longitud de un lado desconocido de un triángulo rectángulo, siempre y cuando conozcamos las longitudes de los otros dos lados.

Sin embargo, existen diferentes formas de aplicar el Teorema de Pitágoras, dependiendo de las variables que conozcamos. A continuación, vamos a ver las 4 fórmulas del Teorema de Pitágoras.

Fórmula 1: Calcular la hipotenusa

La primera fórmula del Teorema de Pitágoras se utiliza para calcular la longitud de la hipotenusa, si conocemos las longitudes de los dos catetos. En este caso, la fórmula quedaría así:

c = √(a² + b²)

Es decir, la longitud de la hipotenusa es igual a la raíz cuadrada de la suma de los cuadrados de los catetos.

Fórmula 2: Calcular un cateto

La segunda fórmula del Teorema de Pitágoras se utiliza para calcular la longitud de uno de los catetos, si conocemos la longitud de la hipotenusa y la longitud del otro cateto. En este caso, la fórmula quedaría así:

a = √(c² - b²)

o bien

b = √(c² - a²)

Es decir, la longitud de un cateto es igual a la raíz cuadrada de la diferencia entre el cuadrado de la hipotenusa y el cuadrado del otro cateto.

Fórmula 3: Calcular la altura de un triángulo rectángulo

La tercera fórmula del Teorema de Pitágoras se utiliza para calcular la altura de un triángulo rectángulo, si conocemos la longitud de la hipotenusa y la longitud de uno de los catetos. En este caso, la fórmula quedaría así:

h = b(a/c)

Donde "h" es la altura del triángulo, "b" es la longitud del cateto conocido y "c" es la longitud de la hipotenusa.

Fórmula 4: Calcular la distancia entre dos puntos en un plano cartesiano

La cuarta fórmula del Teorema de Pitágoras se utiliza para calcular la distancia entre dos puntos en un plano cartesiano. En este caso, la fórmula quedaría así:

d = √((x₂ - x₁)² + (y₂ - y₁)²)

Donde "d" es la distancia entre los dos puntos, "x₁" y "y₁" son las coordenadas del primer punto, y "x₂" y "y₂" son las coordenadas del segundo punto.

Esta fórmula se basa en la idea de que los dos puntos forman los catetos de un triángulo rectángulo, y la distancia entre ellos es la hipotenusa.

Conclusión

El Teorema de Pitágoras es una herramienta muy útil para resolver problemas geométricos. Ahora que conoces las 4 fórmulas del Teorema de Pitágoras, podrás aplicarlas en diferentes situaciones para calcular longitudes, alturas y distancias. Recuerda que siempre es importante entender la teoría detrás de las fórmulas, para poder aplicarlas correctamente.

Preguntas frecuentes

1. ¿Por qué se llama Teorema de Pitágoras?

El Teorema de Pitágoras lleva el nombre del matemático griego Pitágoras, quien se cree que fue el primero en demostrarlo.

2. ¿Qué es un triángulo rectángulo?

Un triángulo rectángulo es un tipo de triángulo que tiene un ángulo recto (90 grados).

3. ¿Cuál es la hipotenusa?

La hipotenusa es el lado más largo de un triángulo rectángulo, y está opuesto al ángulo recto.

4. ¿Para qué se utiliza el Teorema de Pitágoras?

El Teorema de Pitágoras se utiliza para calcular la longitud de los lados de un triángulo rectángulo.

5. ¿En qué situaciones se puede aplicar el Teorema de Pitágoras?

El Teorema de Pitágoras se puede aplicar en situaciones donde tengamos un triángulo rectángulo y necesitemos calcular alguna de sus longitudes, alturas o distancias. También se puede utilizar en problemas de geometría analítica, como el cálculo de distancias en un plano cartesiano.