Descubre las 3 fórmulas del Teorema de Pitágoras
¿Recuerdas tus clases de geometría en la escuela? Seguramente has oído hablar del Teorema de Pitágoras, una de las fórmulas más conocidas en matemáticas. Pero, ¿sabías que existen tres fórmulas diferentes que se derivan de este teorema? En este artículo, te mostraremos las tres fórmulas del Teorema de Pitágoras y cómo aplicarlas en problemas de geometría.
¿Qué es el Teorema de Pitágoras?
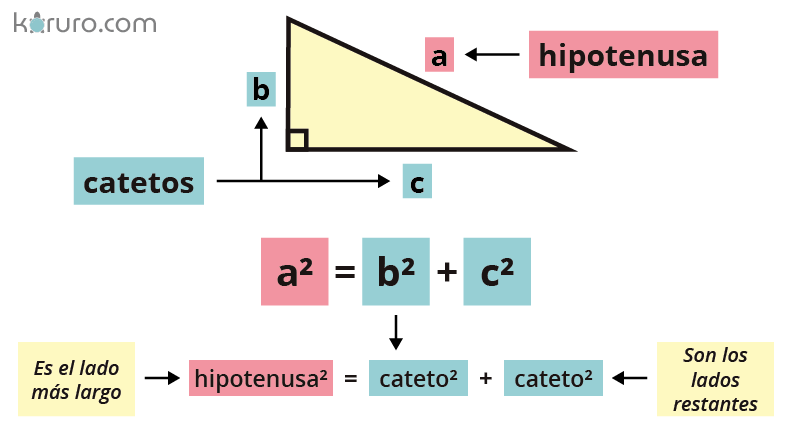
El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. En otras palabras, si a y b son los catetos de un triángulo rectángulo y c es la hipotenusa, entonces:
c^2 = a^2 + b^2
Esta fórmula es muy útil para calcular la longitud de los lados de un triángulo rectángulo cuando conoces la longitud de los otros dos lados.
Fórmula para calcular la hipotenusa
La primera fórmula derivada del Teorema de Pitágoras es la que se utiliza para calcular la longitud de la hipotenusa cuando conoces la longitud de los dos catetos. En este caso, la fórmula sería:
c = √(a^2 + b^2)
Es decir, la longitud de la hipotenusa es igual a la raíz cuadrada de la suma de los cuadrados de los catetos.
Por ejemplo, si conoces que los catetos de un triángulo rectángulo miden 3 y 4 unidades, para encontrar la longitud de la hipotenusa tendrías que aplicar la fórmula de la siguiente manera:
c = √(3^2 + 4^2)
c = √(9 + 16)
c = √25
c = 5
Por lo tanto, la longitud de la hipotenusa de este triángulo rectángulo es de 5 unidades.
Fórmula para calcular un cateto
La segunda fórmula del Teorema de Pitágoras es la que se utiliza para calcular la longitud de uno de los catetos cuando conoces la longitud de la hipotenusa y la longitud del otro cateto. En este caso, la fórmula sería:
a = √(c^2 - b^2)
O bien,
b = √(c^2 - a^2)
Es decir, la longitud de uno de los catetos es igual a la raíz cuadrada de la diferencia entre el cuadrado de la hipotenusa y el cuadrado del otro cateto.
Por ejemplo, si conoces que la hipotenusa de un triángulo rectángulo mide 5 unidades y uno de los catetos mide 3 unidades, para encontrar la longitud del otro cateto tendrías que aplicar la fórmula de la siguiente manera:
b = √(5^2 - 3^2)
b = √(25 - 9)
b = √16
b = 4
Por lo tanto, la longitud del otro cateto de este triángulo rectángulo es de 4 unidades.
Fórmula para calcular el área de un triángulo rectángulo
La tercera fórmula derivada del Teorema de Pitágoras es la que se utiliza para calcular el área de un triángulo rectángulo cuando conoces la longitud de los dos catetos. En este caso, la fórmula sería:
A = (a * b) / 2
Es decir, el área del triángulo rectángulo es igual al producto de los dos catetos dividido entre dos.
Por ejemplo, si conoces que los catetos de un triángulo rectángulo miden 3 y 4 unidades, para encontrar el área del triángulo tendrías que aplicar la fórmula de la siguiente manera:
A = (3 * 4) / 2
A = 6
Por lo tanto, el área de este triángulo rectángulo es de 6 unidades cuadradas.
Conclusión
El Teorema de Pitágoras es una de las fórmulas más importantes en geometría y matemáticas en general. Conocer las tres fórmulas derivadas de este teorema te permitirá resolver problemas de geometría que involucren triángulos rectángulos con mayor facilidad. Recuerda que la fórmula para calcular la hipotenusa te permite encontrar la longitud de la hipotenusa cuando conoces los catetos, la fórmula para calcular un cateto te permite encontrar la longitud de uno de los catetos cuando conoces la hipotenusa y el otro cateto, y la fórmula para calcular el área te permite encontrar el área del triángulo rectángulo cuando conoces los dos catetos.
Preguntas frecuentes
1. ¿Qué es un triángulo rectángulo?
Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90 grados.
2. ¿Cuál es la hipotenusa en un triángulo rectángulo?
La hipotenusa en un triángulo rectángulo es el lado opuesto al ángulo recto y es el lado más largo del triángulo.
3. ¿Por qué es importante el Teorema de Pitágoras?
El Teorema de Pitágoras es importante en matemáticas y geometría porque es una herramienta fundamental para calcular la longitud de los lados de un triángulo rectángulo. Además, se utiliza en muchos campos, como la ingeniería, la arquitectura y la física.
4. ¿Qué otras fórmulas son importantes en geometría?
Además del Teorema de Pitágoras, existen muchas otras fórmulas importantes en geometría, como la fórmula del área de un triángulo (A = b * h / 2), la fórmula del perímetro de un círculo (P = 2 * π * r) y la fórmula del volumen de una esfera (V = 4/3 * π * r^3).
5. ¿Cómo puedo aplicar el Teorema de Pitágoras en la vida cotidiana?
El Teorema de Pitágoras se puede aplicar en la vida cotidiana en situaciones como calcular la distancia entre dos puntos en un mapa, medir la diagonal de una pantalla de televisión o calcular la longitud de un cable necesario para conectar dos puntos.
Deja una respuesta